Why not use hashing/hash tables for everything?

Why Not Use Hashing for Everything? Understanding Hash Table Limitations

Hash tables offer incredible average-case performance, but they aren't a silver bullet. This article explores the scenarios where hash tables fall short and why other data structures are often more suitable.

Hash tables are a fundamental data structure in computer science, renowned for their efficiency in operations like insertion, deletion, and lookup, often achieving an average time complexity of O(1). This makes them incredibly attractive for a wide range of applications, from database indexing to caching and symbol tables in compilers. Given their speed, one might wonder: why not just use hash tables for every data storage and retrieval need? The answer lies in understanding their specific characteristics, advantages, and, crucially, their limitations. While powerful, hash tables are not a panacea and can be suboptimal or even detrimental in certain situations.

The Core Strengths of Hash Tables

Before diving into limitations, it's essential to appreciate what makes hash tables so effective. Their primary strength comes from the hash function, which maps keys to indices in an array (the hash table's underlying storage). When collisions occur (multiple keys mapping to the same index), various strategies like separate chaining or open addressing are used to resolve them. This direct mapping allows for near-instantaneous access to data on average.

flowchart TD
    A[Input Key] --> B{"Hash Function"}
    B --> C{Hash Value (Index)}
    C --> D[Array Slot]
    D --"Collision?"--> E{Collision Resolution}
    E --> F[Store/Retrieve Value]
    F --> G[Output Value]
    E --"No Collision"--> F

Simplified Hash Table Operation Flow

When Hash Tables Fall Short: Key Limitations

Despite their average-case efficiency, hash tables have several inherent drawbacks that make them unsuitable for certain tasks. Understanding these limitations is crucial for choosing the right data structure for your specific problem.

1. Poor Performance for Ordered Data Operations

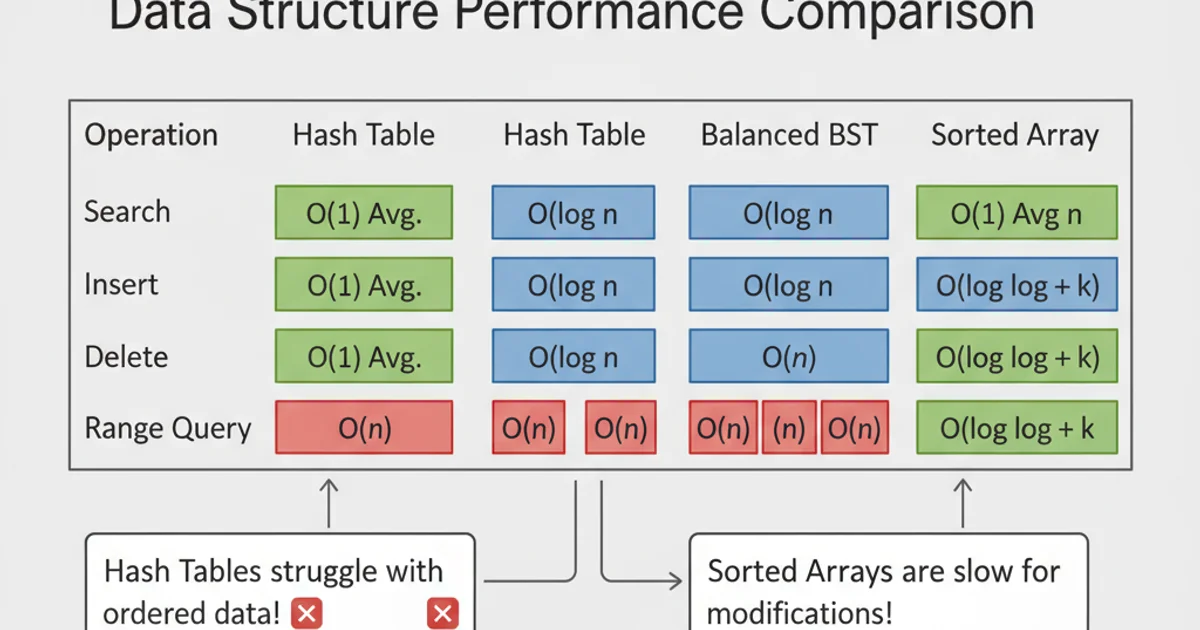
Hash tables are inherently unordered. The order in which elements are inserted or stored bears no relation to their logical order based on key values. This means that operations requiring sorted data, such as finding the minimum/maximum element, range queries (e.g., 'find all elements between X and Y'), or iterating through elements in sorted order, are extremely inefficient. To perform these operations, you would typically have to extract all elements, sort them, and then process them, which negates the O(1) lookup advantage.

my_dict = {"apple": 3, "banana": 1, "cherry": 2}

# Finding min/max key is inefficient
min_key = min(my_dict.keys()) # O(N) to get keys, then O(N) to find min

# Iterating in sorted order requires sorting keys first
for key in sorted(my_dict.keys()):
    print(f"{key}: {my_dict[key]}") # O(N log N) for sorting

Demonstrating inefficient ordered operations in a Python dictionary (hash table).

2. Worst-Case Performance and Collision Handling

While average-case performance is O(1), the worst-case time complexity for hash table operations can degrade to O(N), where N is the number of elements. This occurs when a poorly designed hash function or malicious input leads to a high number of collisions, effectively turning the hash table into a linked list (in the case of separate chaining) or requiring extensive probing (in open addressing). This vulnerability makes hash tables less suitable for applications where guaranteed worst-case performance is critical, such as real-time systems or security-sensitive contexts.

graph TD
    A[Good Hash Function] --> B{Even Distribution}
    B --> C[O(1) Average Time]

    D[Poor Hash Function] --> E{Many Collisions}
    E --> F[O(N) Worst-Case Time]
    F --> G[Performance Degradation]

Impact of Hash Function Quality on Performance

3. Memory Overhead and Resizing

Hash tables often require more memory than other data structures to maintain their performance. They typically need to be larger than the actual number of elements stored to minimize collisions and maintain a low load factor. When the load factor exceeds a certain threshold, the hash table must be resized, which involves allocating a new, larger array and re-hashing all existing elements into the new array. This resizing operation can be very expensive (O(N)) and can cause temporary performance spikes, which might be unacceptable in latency-sensitive applications.

4. Lack of Locality of Reference

Due to the nature of hashing, elements that are logically 'close' (e.g., keys 100, 101, 102) are often scattered across different, non-contiguous memory locations in the hash table's underlying array. This lack of spatial locality can lead to more cache misses, as the CPU has to fetch data from main memory more frequently, potentially slowing down operations compared to data structures like arrays or B-trees that exhibit better locality.

5. Complexities of Hash Function Design

Designing a good hash function is non-trivial. A good hash function should be fast to compute, distribute keys uniformly across the hash table, and minimize collisions. A poorly chosen hash function can severely degrade performance, leading to the O(N) worst-case scenario. For complex objects, defining an effective hash function can be challenging and error-prone.

Alternatives and When to Use Them

Given these limitations, other data structures often provide better solutions for specific problems:

Comparison of Data Structure Strengths

• Balanced Binary Search Trees (e.g., Red-Black Trees, AVL Trees): Ideal for scenarios requiring ordered data operations (min/max, range queries, sorted iteration) while maintaining logarithmic time complexity (O(log N)) for search, insertion, and deletion. They offer guaranteed O(log N) worst-case performance, unlike hash tables.
• Arrays/Vectors: Excellent for sequential access, fixed-size collections, and when element order is important. O(1) access by index, but O(N) for insertion/deletion in the middle.
• Linked Lists: Good for frequent insertions and deletions at arbitrary positions (O(1) if the position is known), but O(N) for search.
• Tries: Efficient for string-based keys, especially for prefix searches and autocomplete functionalities.

In conclusion, while hash tables are incredibly powerful for dictionary-like operations (key-value storage and retrieval) with excellent average-case performance, their lack of inherent order, potential for worst-case performance degradation, memory overhead, and the complexities of hash function design mean they are not universally applicable. A skilled developer understands the strengths and weaknesses of various data structures and chooses the most appropriate one based on the specific requirements of the problem at hand.