Circle covering algorithm with varying radii

Optimizing Circle Covering with Varying Radii

Explore algorithms and strategies for efficiently covering a set of points or an area with circles of different sizes, a common challenge in geometry and optimization.

The circle covering problem, particularly when circles have varying radii, is a fundamental challenge in computational geometry and optimization. It involves finding the minimum number of circles, or circles with minimum total area/cost, to cover a given set of points or a continuous region. This problem has wide-ranging applications, from sensor network deployment and wireless communication coverage to facility location and even art. Unlike the simpler case of identical circles, varying radii introduce significant complexity, requiring more sophisticated algorithmic approaches.

Understanding the Problem: Fixed Points vs. Continuous Regions

Before diving into algorithms, it's crucial to distinguish between two main variants of the circle covering problem with varying radii:

1. Covering a set of discrete points: Here, the goal is to ensure every specified point is within at least one circle. This is often encountered in sensor placement, where each sensor (circle) has a different detection range (radius).
2. Covering a continuous region: This variant aims to cover an entire area, such as a polygon or a complex shape. This is more challenging as it requires ensuring every infinitesimal point within the region is covered, often approximated by covering a dense grid of points or using geometric properties of the region.

The choice of algorithm heavily depends on which of these two scenarios you are addressing, as well as whether the circle centers are fixed or can be chosen optimally.

flowchart TD
    A[Start: Circle Covering Problem] --> B{Varying Radii?}
    B -- Yes --> C{What needs to be covered?}
    C -- Discrete Points --> D[Point Covering Algorithms]
    C -- Continuous Region --> E[Region Covering Algorithms]
    D --> F{Are Circle Centers Fixed?}
    E --> G{Are Circle Centers Fixed?}
    F -- Yes --> H[Greedy, Set Cover Heuristics]
    F -- No --> I[Optimization (e.g., LP, Genetic Algorithms)]
    G -- Yes --> J[Approximation, Grid-based Methods]
    G -- No --> K[Complex Optimization (e.g., Voronoi, Delaunay)]
    H --> L[Solution]
    I --> L
    J --> L
    K --> L

Decision flow for approaching circle covering problems with varying radii.

Algorithmic Approaches for Point Covering

For covering a set of discrete points with varying radii, several algorithmic paradigms can be employed. The complexity often stems from the combinatorial nature of selecting which circles to use and where to place them.

1. Greedy Algorithms

A common starting point, especially when circle centers are pre-defined or limited. A simple greedy strategy might involve:

• Sorting circles by radius (largest first) or by the number of uncovered points they cover.
• Iteratively selecting the circle that covers the most currently uncovered points.
• Removing covered points and repeating until all points are covered.

2. Set Cover Formulation

The point covering problem can be modeled as a variation of the Set Cover Problem, which is NP-hard. Each point is an element, and each available circle represents a set of points it can cover. The goal is to find the minimum number of sets (circles) that cover all elements (points). Approximation algorithms for Set Cover can be adapted here.

3. Optimization Techniques

When circle centers can be chosen, the problem becomes continuous and more complex. Techniques like Linear Programming (LP), Integer Linear Programming (ILP), or metaheuristics such as Genetic Algorithms (GAs) and Simulated Annealing can be used. These methods search for optimal or near-optimal placements and selections of circles.

Example: Simple Greedy Approach (Conceptual)

def greedy_circle_cover(points, circles):
    covered_points = set()
    selected_circles = []
    
    # Sort circles by their potential to cover new points (e.g., largest radius first)
    # For simplicity, let's assume circles are (center_x, center_y, radius)
    # and points are (point_x, point_y)
    circles.sort(key=lambda c: c[2], reverse=True) # Sort by radius descending

    while len(covered_points) < len(points):
        best_circle = None
        max_new_covered = -1
        
        for circle in circles:
            if circle in selected_circles: # Skip already selected circles
                continue

            current_new_covered = 0
            for i, p in enumerate(points):
                if i not in covered_points: # Only consider uncovered points
                    dist_sq = (p[0] - circle[0])**2 + (p[1] - circle[1])**2
                    if dist_sq <= circle[2]**2:
                        current_new_covered += 1
            
            if current_new_covered > max_new_covered:
                max_new_covered = current_new_covered
                best_circle = circle
        
        if best_circle is None: # Cannot cover all points
            break
            
        selected_circles.append(best_circle)
        
        # Update covered points
        for i, p in enumerate(points):
            if i not in covered_points:
                dist_sq = (p[0] - best_circle[0])**2 + (p[1] - best_circle[1])**2
                if dist_sq <= best_circle[2]**2:
                    covered_points.add(i)
                    
    return selected_circles, len(covered_points) == len(points)

A conceptual Python implementation of a greedy algorithm for point covering.

Challenges and Advanced Considerations

The varying radii introduce several complexities:

• Overlap Management: How much overlap is acceptable or desirable? Excessive overlap can be inefficient, while too little might leave gaps or require more circles.
• Computational Cost: As the number of points and circles increases, the combinatorial explosion makes exact solutions intractable. Approximation algorithms and heuristics become essential.
• Dynamic Scenarios: In real-time applications, points or circle properties might change, requiring dynamic updates or re-computation of the covering.
• Cost Functions: Beyond just minimizing the number of circles, objectives might include minimizing total area, total cost (if circles have different costs), or maximizing coverage with a fixed budget.

Advanced techniques often involve geometric data structures like k-d trees or quadtrees to efficiently query points within a given radius, especially when dealing with large datasets. For continuous region covering, methods like Voronoi diagrams or Delaunay triangulations can help identify critical areas that need coverage.

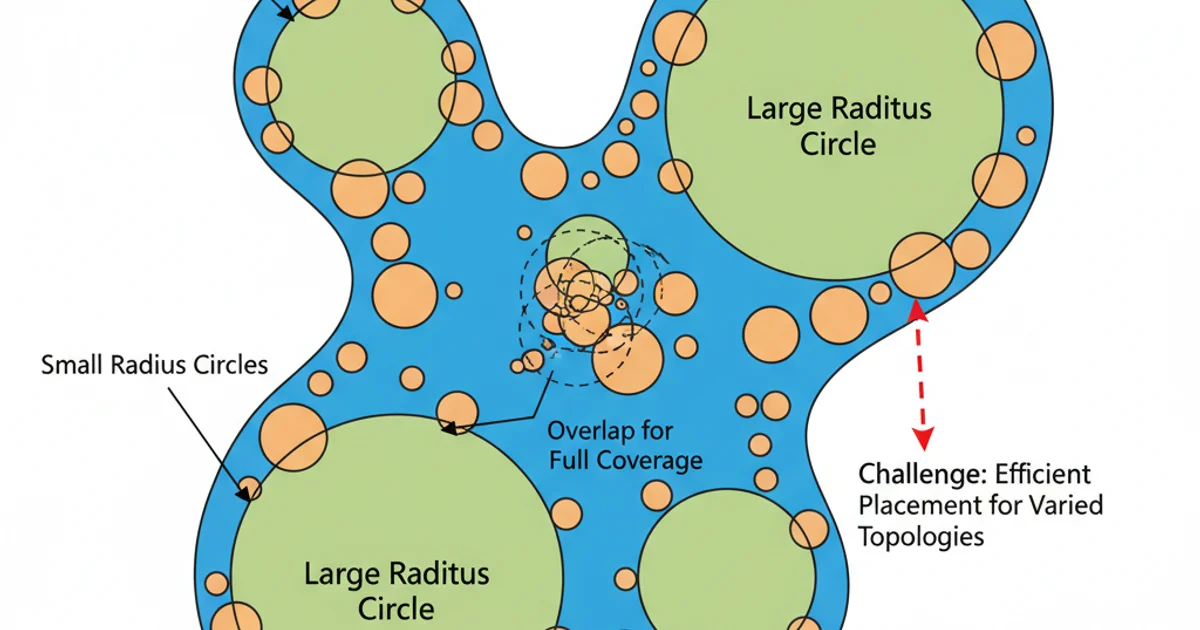
A complex region covered by circles of varying radii, highlighting the challenge of efficient placement.