How to Calculate Circumference of Pipe with Specified Pitch

Calculating the Circumference of a Pipe with a Specified Pitch

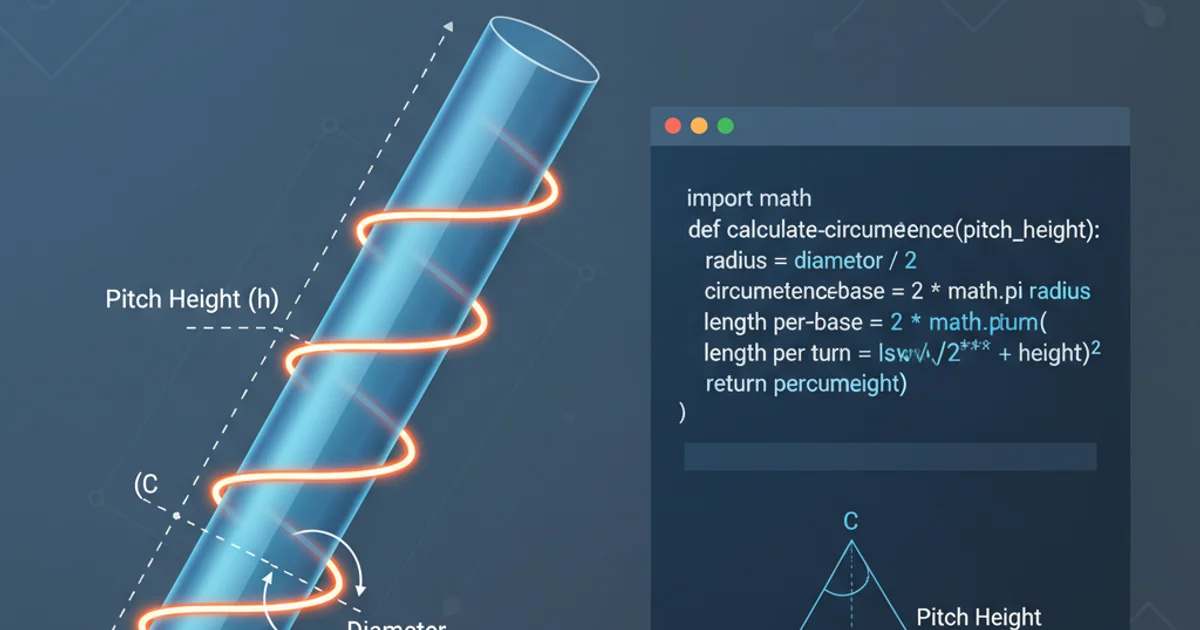
Learn how to accurately calculate the circumference of a pipe when a helical pitch (like a thread or coil) is involved, moving beyond simple circular geometry.

Calculating the circumference of a pipe might seem straightforward – it's simply π * D (pi times diameter). However, this basic formula only applies to a flat, two-dimensional cross-section. When dealing with a pipe that has a specified pitch, such as a threaded pipe, a coiled wire around it, or a helical path, the effective circumference for one full turn along that pitch is no longer just the pipe's outer circumference. Instead, you're calculating the length of a helix for one revolution. This article will guide you through the necessary formulas and considerations to accurately determine this 'pitched circumference'.

Understanding Pitch and Helical Length

Pitch, in this context, refers to the axial distance a point travels along the pipe's axis for one complete revolution around the pipe. Imagine unwrapping one turn of the helix into a right-angled triangle. The base of this triangle would be the pipe's standard circumference, and the height would be the pitch. The hypotenuse of this triangle represents the actual length of one turn of the helix, which is what we're calling the 'circumference with pitch'.

flowchart TD
    A[Start] --> B{Identify Pipe Diameter (D)};
    B --> C{Identify Pitch (P)};
    C --> D[Calculate Standard Circumference (C_std = π * D)];
    D --> E[Apply Pythagorean Theorem (C_pitch = sqrt(C_std^2 + P^2))];
    E --> F[Result: Circumference with Pitch (C_pitch)];
    F --> G[End];

Flowchart for calculating circumference with pitch.

The Formula for Circumference with Pitch

To calculate the length of one turn of a helix (the 'circumference with pitch'), we can use the Pythagorean theorem. Consider one full revolution of the helix. If you were to 'unroll' this section, it would form a right-angled triangle where:

• One leg is the standard circumference of the pipe (C_std = π * D), where D is the pipe's outer diameter.
• The other leg is the pitch (P).
• The hypotenuse is the length of one turn of the helix (C_pitch).

Therefore, the formula is:

C_pitch = √( (π * D)² + P² )

Where:

• C_pitch is the circumference of the pipe with the specified pitch.
• π (pi) is approximately 3.14159.
• D is the outer diameter of the pipe.
• P is the pitch (the axial distance per revolution).

Practical Example

Let's calculate the circumference with pitch for a pipe with an outer diameter of 50 mm and a pitch of 10 mm.

import math

# Given values
diameter = 50  # mm
pitch = 10     # mm

# Step 1: Calculate standard circumference
standard_circumference = math.pi * diameter
print(f"Standard Circumference: {standard_circumference:.2f} mm")

# Step 2: Calculate circumference with pitch
circumference_with_pitch = math.sqrt(standard_circumference**2 + pitch**2)
print(f"Circumference with Pitch: {circumference_with_pitch:.2f} mm")

# Expected Output:
# Standard Circumference: 157.08 mm
# Circumference with Pitch: 157.40 mm

Python code to calculate circumference with pitch.

As you can see from the example, the 'circumference with pitch' is slightly longer than the standard circumference, which makes intuitive sense as it accounts for the axial travel per revolution.