loop tiling. how to choose block size?

Optimizing Loop Performance: The Art of Choosing Block Size in Loop Tiling

Explore loop tiling, a powerful optimization technique for CPU cache utilization. Learn how to strategically select block sizes to significantly enhance the performance of your C programs.

Loop tiling, also known as loop blocking, is a compiler optimization technique that attempts to improve the cache performance of a program. It reorganizes the iteration space of a loop nest into smaller, contiguous blocks, or 'tiles'. The goal is to ensure that data accessed within a tile remains in the faster cache memory for as long as possible, reducing the number of costly main memory accesses. This article delves into the intricacies of loop tiling, with a particular focus on the critical decision of choosing an optimal block size.

Understanding Loop Tiling and Cache Locality

Modern CPUs operate with a hierarchical memory system, where smaller, faster caches (L1, L2, L3) sit between the CPU and slower main memory (RAM). The performance gap between CPU and RAM is vast, making cache misses a major bottleneck. Loop tiling addresses this by improving both temporal and spatial locality.

Temporal locality refers to the reuse of data within a short period. By processing a small block of data entirely before moving to the next, tiled loops maximize the chances that data remains in cache for subsequent operations. Spatial locality refers to accessing data items that are physically close to each other in memory. Tiling helps by processing contiguous chunks of data, which are often loaded into cache lines together.

Consider a matrix multiplication operation. Without tiling, an inner loop might repeatedly access elements from a row of one matrix and a column of another, potentially evicting useful data from cache before it can be reused. Tiling ensures that a sub-matrix (a 'tile') of each operand is loaded into cache and processed completely, leading to significant performance gains.

flowchart TD
    A[Original Loop Nest] --> B{Data Access Pattern}
    B --> C[High Cache Miss Rate]
    C --> D[Poor Performance]

    A --> E[Loop Tiling Applied]
    E --> F{Blocked Data Access}
    F --> G[Improved Cache Locality]
    G --> H[Reduced Cache Misses]
    H --> I[Enhanced Performance]

Impact of Loop Tiling on Cache Performance

The Critical Role of Block Size

The block size is the most crucial parameter in loop tiling. An improperly chosen block size can negate the benefits of tiling or even degrade performance. The ideal block size is a delicate balance, primarily dictated by the size of your CPU's cache levels and the data types being processed.

If the block size is too small, the overhead of managing the tiles might outweigh the cache benefits. If it's too large, the tile will not fit entirely into the target cache level, leading to cache misses within the tile itself, defeating the purpose of tiling. The goal is to select a block size such that the working set of data for a single tile fits comfortably within a specific cache level (typically L1 or L2).

For example, in matrix multiplication C = A * B, a tile operation involves a sub-matrix of A, a sub-matrix of B, and a sub-matrix of C. The combined size of these three sub-matrices must fit into the cache. If A, B, and C are N x N matrices of double (8 bytes), and we are tiling with block size B, then the working set for a tile is approximately 3 * B * B * sizeof(double) bytes. This value should be less than the target cache size.

Strategies for Choosing an Optimal Block Size

Determining the optimal block size is often an empirical process, but several strategies can guide your choice:

1. Cache Size Awareness: The most fundamental approach is to know your target CPU's cache sizes (L1, L2, L3). Tools like lscpu on Linux can provide this information. Aim for a block size that allows the working set of a tile to fit within the L1 or L2 cache. L1 cache is usually the fastest, but also the smallest.

2. Power of Two: Block sizes that are powers of two (e.g., 16, 32, 64) often align well with cache line sizes and memory addressing schemes, potentially leading to better performance.

3. Empirical Tuning (Trial and Error): This is often the most effective method. Start with a reasonable estimate based on cache sizes and then systematically test different block sizes around that estimate. Measure performance (e.g., execution time, cache miss rate) for each block size to find the sweet spot. This is especially important as optimal block size can vary based on the specific algorithm, data access patterns, and even compiler optimizations.

4. Compiler Optimizations: Modern compilers (like GCC with -O3 or -Ofast) often perform automatic loop tiling. While this can be effective, manual tiling gives you finer control, especially for complex access patterns or when targeting specific cache levels. It's worth comparing manual tiling performance against compiler-optimized versions.

5. Data Layout: The memory layout of your data (row-major vs. column-major) can influence the effectiveness of tiling. Ensure your tiling strategy aligns with how your data is stored to maximize spatial locality.

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

#define N 1024 // Matrix dimension

// Function to perform matrix multiplication with tiling
void multiply_tiled(double *A, double *B, double *C, int block_size) {
    for (int i = 0; i < N; i += block_size) {
        for (int j = 0; j < N; j += block_size) {
            for (int k = 0; k < N; k += block_size) {
                // Blocked matrix multiplication
                for (int ii = i; ii < i + block_size && ii < N; ++ii) {
                    for (int jj = j; jj < j + block_size && jj < N; ++jj) {
                        for (int kk = k; kk < k + block_size && kk < N; ++kk) {
                            C[ii * N + jj] += A[ii * N + kk] * B[kk * N + jj];
                        }
                    }
                }
            }
        }
    }
}

// Function to perform matrix multiplication without tiling
void multiply_untiled(double *A, double *B, double *C) {
    for (int i = 0; i < N; ++i) {
        for (int j = 0; j < N; ++j) {
            for (int k = 0; k < N; ++k) {
                C[i * N + j] += A[i * N + k] * B[k * N + j];
            }
        }
    }
}

int main() {
    double *A = (double *)malloc(N * N * sizeof(double));
    double *B = (double *)malloc(N * N * sizeof(double));
    double *C_tiled = (double *)calloc(N * N, sizeof(double));
    double *C_untiled = (double *)calloc(N * N, sizeof(double));

    // Initialize matrices with random values
    for (int i = 0; i < N * N; ++i) {
        A[i] = (double)rand() / RAND_MAX;
        B[i] = (double)rand() / RAND_MAX;
    }

    // Test untiled multiplication
    clock_t start = clock();
    multiply_untiled(A, B, C_untiled);
    clock_t end = clock();
    double untiled_time = (double)(end - start) / CLOCKS_PER_SEC;
    printf("Untiled multiplication time: %f seconds\n", untiled_time);

    // Test tiled multiplication with a sample block size
    int block_size = 32; // Example block size
    start = clock();
    multiply_tiled(A, B, C_tiled, block_size);
    end = clock();
    double tiled_time = (double)(end - start) / CLOCKS_PER_SEC;
    printf("Tiled multiplication (block_size=%d) time: %f seconds\n", block_size, tiled_time);

    // Free memory
    free(A);
    free(B);
    free(C_tiled);
    free(C_untiled);

    return 0;
}

C code demonstrating tiled vs. untiled matrix multiplication. The block_size variable is key for performance tuning.

Advanced Considerations and Tools

Beyond basic cache sizes, several advanced factors can influence optimal block size:

• Cache Associativity: Direct-mapped, set-associative, or fully associative caches behave differently. A block size that causes too many conflict misses (where multiple active data blocks map to the same cache set) can degrade performance.
• TLB (Translation Lookaside Buffer): The TLB caches virtual-to-physical address translations. Very large block sizes might lead to TLB misses, adding another layer of overhead.
• Multi-threading/Parallelism: When using multiple threads, each thread's working set must consider the shared cache resources. The optimal block size might need to be adjusted to prevent cache contention between threads.
• Profiling Tools: Tools like perf on Linux, Intel VTune Amplifier, or AMD CodeXL can provide detailed insights into cache miss rates, CPU cycles, and other performance metrics. These tools are invaluable for empirically determining the best block size and identifying performance bottlenecks.

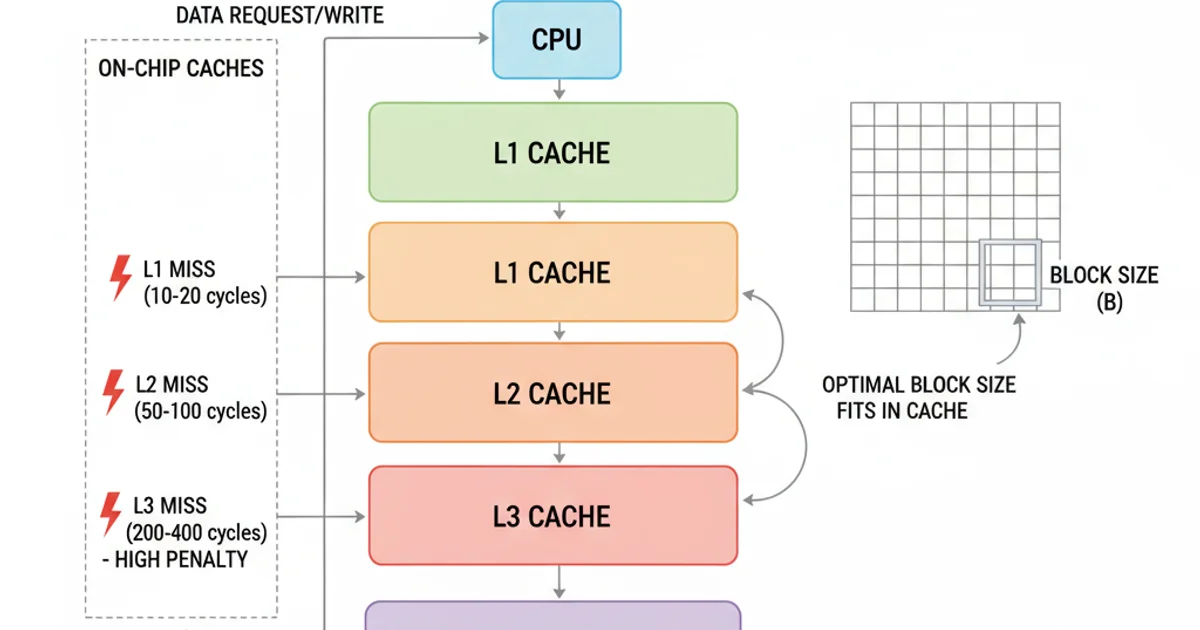
Hierarchical memory system and the impact of cache misses.

In conclusion, loop tiling is a powerful optimization for improving cache utilization and overall program performance. The choice of block size is paramount and requires a blend of theoretical understanding (CPU architecture, cache sizes) and empirical tuning. By carefully selecting and testing block sizes, developers can unlock significant speedups in computationally intensive applications.