Big O confusion: log2(N) vs log3(N)

Big O Notation: Demystifying log2(N) vs. log3(N)

Explore the nuances of logarithmic Big O notation, understanding why the base of the logarithm doesn't typically matter in complexity analysis and when it might.

When analyzing the efficiency of algorithms, Big O notation is our primary tool. It describes how the runtime or space requirements of an algorithm grow as the input size (N) increases. A common point of confusion arises with logarithmic complexities, specifically when comparing log2(N) and log3(N). Many developers wonder if the base of the logarithm matters. This article will clarify why, in most Big O contexts, it doesn't, and when you might encounter scenarios where it could be relevant.

The Core Principle: Change of Base Formula

The key to understanding why the base of the logarithm is often ignored in Big O notation lies in the change of base formula for logarithms. This fundamental mathematical identity states that for any positive numbers a, b, and x (where a ≠ 1 and b ≠ 1):

log_a(x) = log_b(x) / log_b(a)

Let's apply this to log2(N) and log3(N):

log2(N) = log3(N) / log3(2)

Here, log3(2) is a constant value (approximately 0.63). This means that log2(N) is simply log3(N) multiplied by a constant factor. Similarly, log3(N) is log2(N) multiplied by log2(3) (approximately 1.58).

flowchart TD
    A["Input Size N"]
    B["Algorithm A (log2(N))"]
    C["Algorithm B (log3(N))"]
    D["Change of Base Formula"]
    E["Constant Factor (log_b(a))"]
    F["Big O Equivalence"]

    A --> B
    A --> C
    B -- "Relates via" --> D
    C -- "Relates via" --> D
    D --> E
    E -- "Ignored in Big O" --> F
    B -- "O(log N)" --> F
    C -- "O(log N)" --> F

Illustrating how the change of base formula leads to Big O equivalence for different logarithmic bases.

Why Constant Factors Are Ignored in Big O

Big O notation is concerned with the asymptotic behavior of an algorithm – how its performance scales as N approaches infinity. It provides an upper bound on the growth rate. Constant factors, while important for actual runtime in specific implementations, do not affect the overall growth rate. An algorithm that takes 2 * N operations still grows linearly, just like one that takes 5 * N operations. Both are O(N).

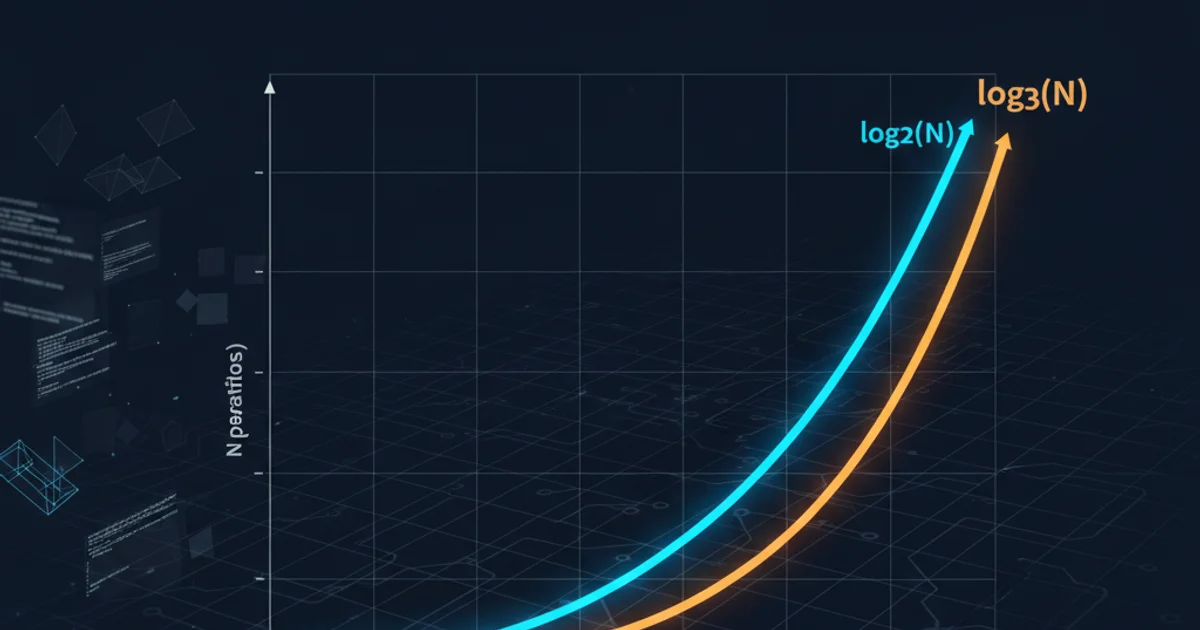
In the same vein, an algorithm with log2(N) operations and one with log3(N) operations both exhibit logarithmic growth. The constant factor log3(2) (or log2(3)) simply shifts the curve up or down, but it doesn't change its fundamental logarithmic shape or its rate of growth relative to other functions like linear (N) or quadratic (N^2). Therefore, both O(log2(N)) and O(log3(N)) are simplified to O(log N).

When the Base Might (Slightly) Matter

While the base is generally ignored in theoretical Big O analysis, there are niche scenarios where it might be mentioned or have a subtle implication:

1. Specific Algorithm Context: Some algorithms inherently operate on a specific base. For example, binary search typically divides the problem space in half, leading to log2(N) operations. A ternary search, which divides into thirds, would lead to log3(N). While both are O(log N), specifying the base can provide more precise information about the algorithm's mechanics.

2. Practical Performance (Constant Factors): In real-world applications, especially for smaller N, the constant factor does matter. An algorithm with log2(N) operations will generally be faster than one with log3(N) operations for the same N because log2(N) grows faster than log3(N) (meaning log2(N) will be a larger number, but log3(N) will require more steps to reach the same value, if that makes sense). For example, log2(1024) = 10, while log3(1024) ≈ 6.3. So, if an operation takes log2(N) steps, it's 10 steps. If it takes log3(N) steps, it's ~6.3 steps. This means log3(N) is actually faster than log2(N) for the same N, as it reaches the solution in fewer divisions. The constant factor log2(3) (approx 1.58) means log2(N) is roughly 1.58 times slower than log3(N).

3. Information Theory: In fields like information theory, the base of the logarithm is crucial. For instance, entropy is often calculated using log2 when dealing with bits of information.

However, these are typically considerations beyond the scope of standard Big O complexity comparison.

import math

def binary_search_steps(n):
    """Simulates steps for binary search (log base 2)"""
    if n <= 0: return 0
    return math.ceil(math.log2(n))

def ternary_search_steps(n):
    """Simulates steps for ternary search (log base 3)"""
    if n <= 0: return 0
    return math.ceil(math.log(n, 3))

N_value = 1000000 # One million elements

print(f"N = {N_value}")
print(f"Binary Search (log2): {binary_search_steps(N_value)} steps")
print(f"Ternary Search (log3): {ternary_search_steps(N_value)} steps")

# Demonstrating the constant factor relationship
log2_of_N = math.log2(N_value)
log3_of_N = math.log(N_value, 3)

print(f"\nlog2({N_value}) = {log2_of_N:.2f}")
print(f"log3({N_value}) = {log3_of_N:.2f}")
print(f"log2({N_value}) / log3({N_value}) = {log2_of_N / log3_of_N:.2f} (approx log2(3))")
print(f"log3({N_value}) / log2({N_value}) = {log3_of_N / log2_of_N:.2f} (approx log3(2))")

Python example demonstrating the number of steps for binary vs. ternary search and the constant factor relationship between log2(N) and log3(N).