SML map function

Mastering the SML map Function: A Deep Dive into Functional Programming

Explore the map function in Standard ML (SML), understanding its mechanics, currying, partial application, and practical uses for list transformations.

The map function is a cornerstone of functional programming, enabling elegant and concise transformations of data structures, particularly lists. In Standard ML (SML), map is a powerful higher-order function that applies a given function to each element of a list, returning a new list containing the results. This article will delve into the map function in SML, covering its definition, usage, and the underlying concepts of currying and partial application that make it so flexible.

Understanding the map Function in SML

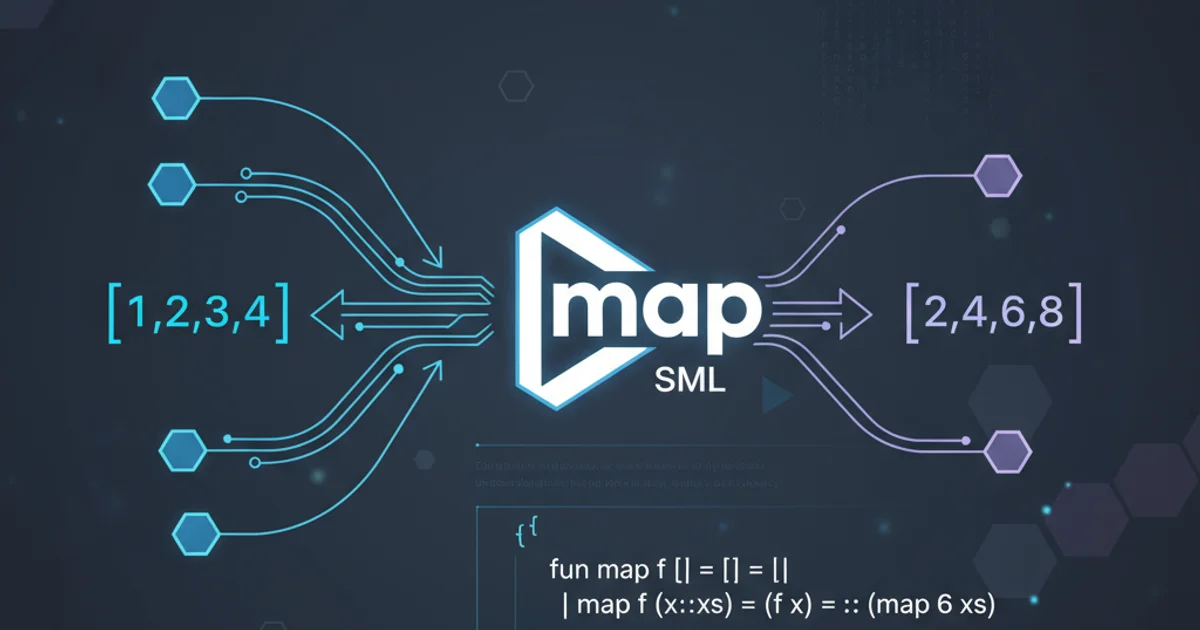
In SML, the map function is typically found within the List structure. Its type signature reveals its higher-order nature: it takes a function ('a -> 'b) and a list of type 'a list, and produces a list of type 'b list. This means it can transform a list of any type 'a into a list of any type 'b, as long as the provided function can perform that transformation.

val map : ('a -> 'b) -> 'a list -> 'b list

Type signature of the map function in SML.

Let's break down this type signature:

• ('a -> 'b): This is the type of the function that map expects as its first argument. It's a function that takes an element of type 'a and returns an element of type 'b.
• 'a list: This is the type of the input list. Its elements must match the input type of the transformation function.
• 'b list: This is the type of the output list. Its elements will be of the type returned by the transformation function.

Practical Examples of map

The versatility of map shines through in various scenarios. Here are some common use cases:

(* Example 1: Doubling each element in a list of integers *)
val doubled_list = List.map (fn x => x * 2) [1, 2, 3, 4];
(* val doubled_list = [2, 4, 6, 8] : int list *)

(* Example 2: Converting a list of integers to a list of strings *)
val string_list = List.map Int.toString [10, 20, 30];
(* val string_list = ["10", "20", "30"] : string list *)

(* Example 3: Applying a more complex transformation *)
val squared_plus_one = List.map (fn x => (x * x) + 1) [1, 2, 3];
(* val squared_plus_one = [2, 5, 10] : int list *)

Basic usage of List.map for various transformations.

Currying and Partial Application with map

SML functions are inherently curried, meaning a function that appears to take multiple arguments actually takes them one at a time, returning a new function at each step until all arguments are supplied. This property is crucial for understanding how map can be used with partial application.

flowchart LR
    A["List.map (fn x => x * 2)"] --> B["Returns a new function: 'int list -> int list'"]
    B --> C["This new function is then applied to [1, 2, 3, 4]"]
    C --> D["Result: [2, 4, 6, 8]"]

Illustrating the currying process of List.map.

When you call List.map (fn x => x * 2), you are not immediately applying map to a list. Instead, you are providing only the first argument (the transformation function). List.map then returns a new function that is specialized to double integers. This new function then waits for its list argument.

val doubler = List.map (fn x => x * 2);
(* val doubler = fn : int list -> int list *)

val result1 = doubler [1, 2, 3];
(* val result1 = [2, 4, 6] : int list *)

val result2 = doubler [5, 6];
(* val result2 = [10, 12] : int list *)

Demonstrating partial application with List.map.

Implementing map (for understanding)

While List.map is built-in, understanding its recursive implementation can deepen your grasp of how it works. A simple version of map can be defined as follows:

fun myMap f [] = []
  | myMap f (x::xs) = (f x) :: (myMap f xs);

(* Example usage *)
val mapped_values = myMap (fn x => x + 10) [1, 2, 3];
(* val mapped_values = [11, 12, 13] : int list *)

A recursive implementation of the map function.

This implementation clearly shows the recursive nature: if the list is empty, return an empty list. Otherwise, apply the function f to the head of the list (x), and prepend the result to the recursively mapped tail of the list (xs).