How to calculate the inverse of the normal cumulative distribution function in python?

Learn how to calculate the inverse of the normal cumulative distribution function in python? with practical examples, diagrams, and best practices. Covers python, scipy, normal-distribution develop...
Tags:
Categories:

Calculating the Inverse Normal CDF in Python

A conceptual image showing a normal distribution curve with a shaded area representing a probability, and an arrow pointing from the shaded area to a specific x-value on the horizontal axis, illustrating the inverse CDF. The curve is blue, the shaded area is light blue, and the axes are black. Clean, technical style.

Learn how to compute the inverse of the normal cumulative distribution function (CDF) in Python using the SciPy library, a crucial operation in statistics and data science.

The normal distribution, also known as the Gaussian distribution, is a fundamental concept in statistics. Its cumulative distribution function (CDF) gives the probability that a random variable will take a value less than or equal to a given value. The inverse of the normal CDF, often called the quantile function or percent point function (PPF), does the opposite: given a probability, it returns the value below which that probability occurs. This operation is essential for tasks like calculating confidence intervals, hypothesis testing, and simulating normally distributed data.

Understanding the Inverse Normal CDF (PPF)

The normal CDF, denoted as ( \Phi(x) ), calculates the probability ( P(X \le x) ) for a normally distributed random variable ( X ). The inverse normal CDF, or PPF, denoted as ( \Phi^{-1}(p) ), takes a probability ( p ) (between 0 and 1) as input and returns the corresponding x-value such that ( P(X \le x) = p ). In simpler terms, if you know the percentile, the PPF tells you the value at that percentile.

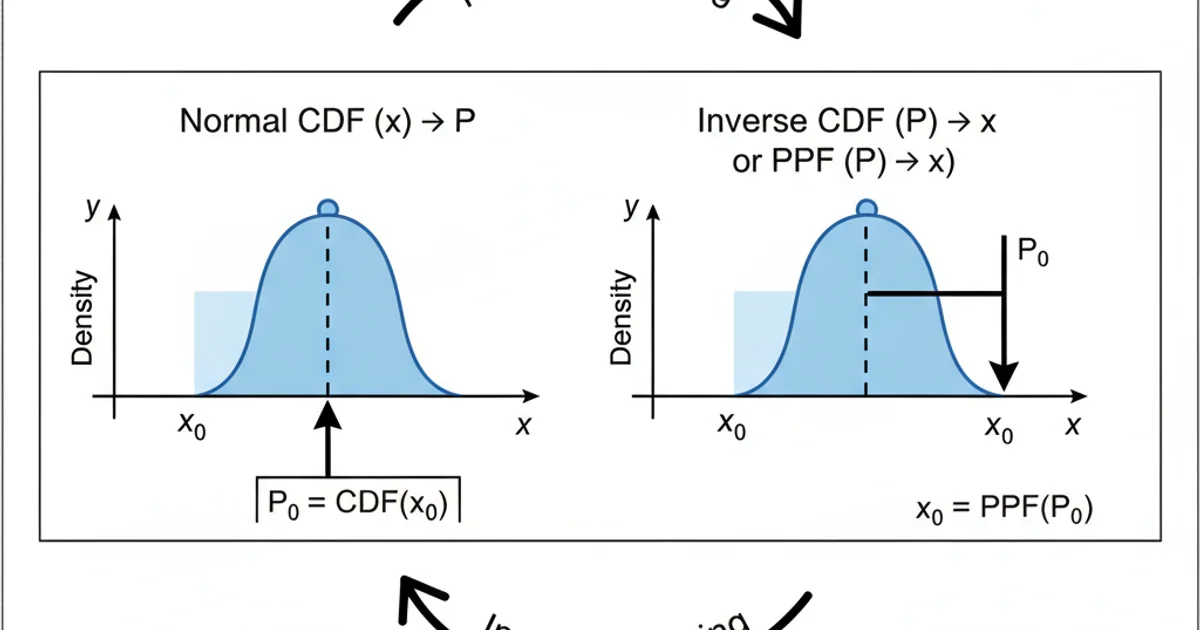
A diagram illustrating the relationship between the Normal CDF and its inverse (PPF). On the left, a normal distribution curve with an x-value pointing to a shaded area representing probability. On the right, the inverse operation: a probability value pointing to an x-value on the same curve. Arrows show the forward and inverse mapping. Use blue for the curve, light blue for shaded areas, and black for axes and labels. Clean, technical style.

Visualizing the Normal CDF and its Inverse (PPF)

Using SciPy for Inverse Normal CDF

Python's SciPy library provides a comprehensive set of statistical functions, including the inverse normal CDF. The scipy.stats.norm module contains methods for various operations related to the normal distribution. The ppf method is specifically designed to calculate the percent point function (inverse CDF).

from scipy.stats import norm

# Calculate the value at the 50th percentile (median) of a standard normal distribution
# A standard normal distribution has mean=0 and standard deviation=1
probability = 0.5
x_value = norm.ppf(probability)
print(f"The value at the {probability*100:.0f}th percentile is: {x_value:.4f}")

# Calculate the value at the 97.5th percentile for a standard normal distribution
# This is often used for 95% confidence intervals (two-tailed)
probability_upper = 0.975
x_value_upper = norm.ppf(probability_upper)
print(f"The value at the {probability_upper*100:.1f}th percentile is: {x_value_upper:.4f}")

# Calculate the value at the 2.5th percentile for a standard normal distribution
probability_lower = 0.025
x_value_lower = norm.ppf(probability_lower)
print(f"The value at the {probability_lower*100:.1f}th percentile is: {x_value_lower:.4f}")

Basic usage of scipy.stats.norm.ppf for a standard normal distribution

Handling Non-Standard Normal Distributions

The norm.ppf method can also handle normal distributions with a specified mean (( \mu )) and standard deviation (( \sigma )). You can pass these parameters directly to the ppf function using the loc (mean) and scale (standard deviation) arguments.

from scipy.stats import norm

# Example: A normal distribution with mean = 100 and standard deviation = 15 (e.g., IQ scores)
mean = 100
std_dev = 15

# What IQ score corresponds to the 84th percentile?
probability = 0.8413
x_value_iq = norm.ppf(probability, loc=mean, scale=std_dev)
print(f"An IQ score at the {probability*100:.2f}th percentile is approximately: {x_value_iq:.2f}")

# What IQ score corresponds to the 16th percentile?
probability_lower_iq = 0.1587
x_value_iq_lower = norm.ppf(probability_lower_iq, loc=mean, scale=std_dev)
print(f"An IQ score at the {probability_lower_iq*100:.2f}th percentile is approximately: {x_value_iq_lower:.2f}")

Calculating inverse CDF for a non-standard normal distribution

Practical Applications

The inverse normal CDF is widely used in various fields:

  • Confidence Intervals: Determining the critical values for constructing confidence intervals for population parameters.
  • Hypothesis Testing: Finding the critical region boundaries for statistical tests.
  • Value at Risk (VaR): In finance, calculating the maximum expected loss over a given period at a certain confidence level.
  • Data Generation: Simulating random data that follows a normal distribution by applying the inverse CDF to uniformly distributed random numbers.

1. Import norm from scipy.stats

Begin by importing the necessary statistical module from SciPy.

2. Define Probability

Specify the probability (quantile) for which you want to find the corresponding x-value. This value must be between 0 and 1.

3. Call norm.ppf()

Use norm.ppf(probability, loc=mean, scale=std_dev) to get the inverse CDF value. For a standard normal distribution, loc defaults to 0 and scale defaults to 1.