Boolean Algebra Simplification (Exam Prep)

Mastering Boolean Algebra Simplification for Exam Success

Unlock the secrets of Boolean algebra simplification. This guide covers fundamental laws, Karnaugh maps, and practical techniques to ace your exams.

Boolean algebra is a fundamental concept in digital electronics, computer science, and discrete mathematics. It provides a systematic way to analyze and design digital circuits and logical expressions. For exam preparation, mastering Boolean algebra simplification is crucial, as it allows you to reduce complex expressions into their simplest forms, making them easier to understand, implement, and evaluate. This article will guide you through the essential laws, theorems, and techniques, including Karnaugh maps, to help you confidently tackle simplification problems.

Fundamental Laws and Theorems of Boolean Algebra

Before diving into simplification techniques, it's essential to have a solid understanding of the basic laws and theorems of Boolean algebra. These rules are the building blocks for manipulating and simplifying expressions. They are often used in conjunction with each other to achieve the desired simplification. Remember that + denotes logical OR, . denotes logical AND (often omitted), and ' denotes logical NOT.

graph TD
    A[Boolean Laws] --> B{Identity Law}
    A --> C{Idempotent Law}
    A --> D{Commutative Law}
    A --> E{Associative Law}
    A --> F{Distributive Law}
    A --> G{Absorption Law}
    A --> H{De Morgan's Theorem}
    B -- "A + 0 = A" --> B1[OR Identity]
    B -- "A . 1 = A" --> B2[AND Identity]
    C -- "A + A = A" --> C1[OR Idempotent]
    C -- "A . A = A" --> C2[AND Idempotent]
    D -- "A + B = B + A" --> D1[OR Commutative]
    D -- "A . B = B . A" --> D2[AND Commutative]
    E -- "A + (B + C) = (A + B) + C" --> E1[OR Associative]
    E -- "A . (B . C) = (A . B) . C" --> E2[AND Associative]
    F -- "A . (B + C) = (A . B) + (A . C)" --> F1[AND Distributive]
    F -- "A + (B . C) = (A + B) . (A + C)" --> F2[OR Distributive]
    G -- "A + (A . B) = A" --> G1[OR Absorption]
    G -- "A . (A + B) = A" --> G2[AND Absorption]
    H -- "(A + B)' = A' . B'" --> H1[De Morgan's OR]
    H -- "(A . B)' = A' + B'" --> H2[De Morgan's AND]

Overview of fundamental Boolean algebra laws and theorems.

Simplification Using Algebraic Manipulation

Algebraic manipulation involves applying the Boolean laws and theorems directly to an expression to simplify it. This method requires a good understanding of the rules and often involves trial and error to find the most efficient path to simplification. The goal is to reduce the number of literals (variables or their complements) and terms in the expression.

Example: Simplify F = A'BC + A'BC' + AB

1. F = A'B(C + C') + AB  (Distributive Law)
2. F = A'B(1) + AB       (Complement Law: C + C' = 1)
3. F = A'B + AB          (Identity Law: X . 1 = X)
4. F = B(A' + A)         (Distributive Law)
5. F = B(1)              (Complement Law: A' + A = 1)
6. F = B                 (Identity Law: X . 1 = X)

Simplified expression: F = B

Step-by-step algebraic simplification of a Boolean expression.

Simplification Using Karnaugh Maps (K-Maps)

Karnaugh Maps (K-Maps) provide a graphical method for simplifying Boolean expressions. They are particularly effective for expressions with 2, 3, or 4 variables, though they can be extended to 5 or 6 variables with increased complexity. K-Maps eliminate the need for extensive algebraic manipulation by visually grouping adjacent '1's (minterms) in a truth table representation. The key is to identify the largest possible groups of 1s that are powers of two (2, 4, 8, etc.).

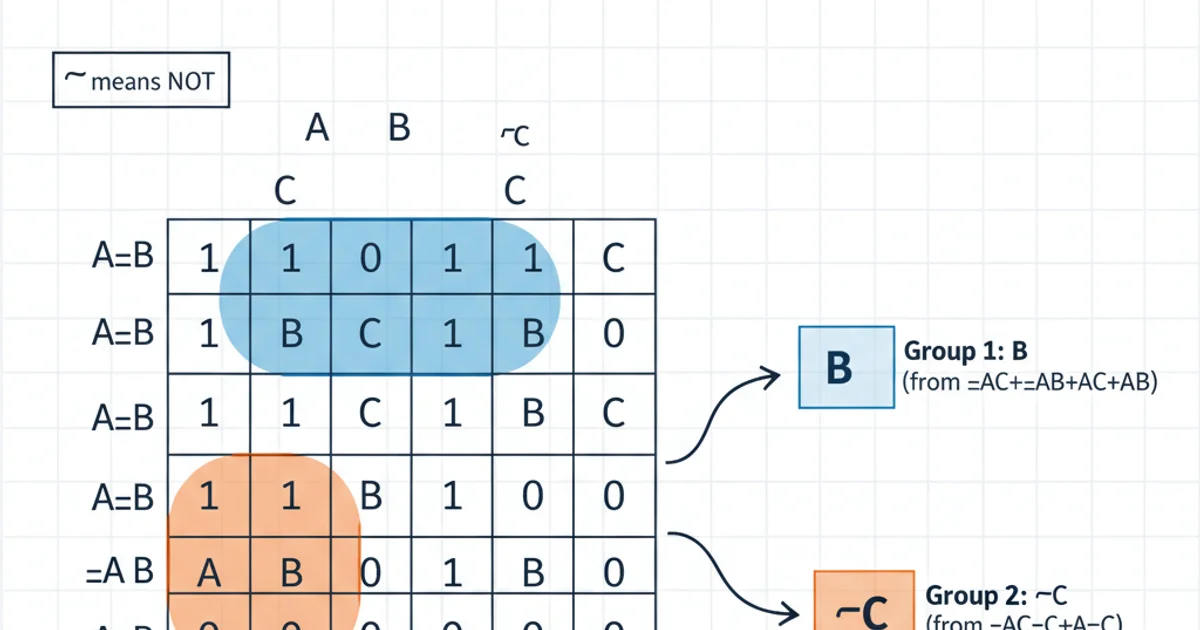
A 3-variable K-Map showing how adjacent '1's are grouped to simplify the expression. The gray code ordering (00, 01, 11, 10) is crucial for adjacency.

1. Construct the K-Map

Draw a K-Map grid based on the number of variables (e.g., 2x2 for 2 variables, 2x4 for 3 variables, 4x4 for 4 variables). Label the rows and columns using Gray code (only one bit changes between adjacent cells).

2. Fill the K-Map

Place '1's in the cells corresponding to the minterms (product terms where the output is '1') of your Boolean expression. Place '0's for minterms where the output is '0', or leave them blank if only '1's are considered.

3. Group the '1's

Identify and group adjacent '1's in powers of two (2, 4, 8, etc.). Groups can wrap around the edges of the map. Aim for the largest possible groups to achieve maximum simplification. Each '1' must be part of at least one group.

4. Derive the Simplified Expression

For each group, identify the variables that remain constant within that group. These constant variables form a product term. Combine these product terms with OR operators to get the final simplified Sum-of-Products (SOP) expression.