Practical Uses of Fractals in Programming

Practical Uses of Fractals in Programming

Explore how fractals, with their self-similar patterns, can be applied in programming for graphics, data compression, and algorithmic generation.

Fractals are fascinating mathematical constructs characterized by self-similarity across different scales. This means that if you zoom into a part of a fractal, it often looks similar to the whole. While often associated with beautiful, complex images, fractals have practical applications in various programming domains, from generating realistic landscapes to optimizing data storage. This article delves into how these intricate patterns can be harnessed in software development.

Generating Complex Graphics and Textures

One of the most intuitive applications of fractals in programming is in computer graphics. Their ability to generate infinite detail from simple rules makes them ideal for creating natural-looking textures, landscapes, and special effects. Fractal algorithms can simulate mountains, clouds, coastlines, and even organic structures with remarkable realism, often requiring less storage than traditional texture mapping methods.

def mandelbrot(c, max_iter):
    z = 0
    n = 0
    while abs(z) <= 2 and n < max_iter:
        z = z*z + c
        n += 1
    return n

# Example usage for a single point
# c = complex(-0.7, 0.27015)
# iterations = mandelbrot(c, 100)
# print(f"Iterations for {c}: {iterations}")

Python function to calculate Mandelbrot set iterations for a given complex number.

flowchart TD
    A[Start Fractal Generation] --> B{Choose Fractal Type}
    B --> C{Mandelbrot Set}
    B --> D{Julia Set}
    B --> E{Iterated Function System (IFS)}
    C --> F[Define Complex Plane Region]
    D --> F
    E --> G[Define Transformation Functions]
    F --> H{Iterate Function for Each Pixel}
    G --> H
    H --> I[Map Iteration Count to Color]
    I --> J[Render Image]
    J --> K[End Fractal Generation]

General workflow for generating fractal images.

Fractal Compression and Data Storage

Fractal image compression is a lossy compression method that leverages the self-similarity within an image. Instead of storing pixel data directly, it stores a set of fractal transforms (Iterated Function Systems or IFS) that, when applied repeatedly, reconstruct the image. This can lead to very high compression ratios, especially for images with significant self-similarity, like natural scenes. While computationally intensive for encoding, decoding is relatively fast.

Randomness, Noise, and Procedural Generation

Fractals are also fundamental to procedural generation, especially in creating realistic noise functions. Perlin noise, for example, is a gradient noise function that generates natural-looking textures and patterns by combining multiple octaves of noise, each with different frequencies and amplitudes. This technique is widely used in game development for terrain generation, cloud rendering, and material textures, providing organic randomness that avoids repetitive tiling.

public float PerlinNoise(float x, float y, int octaves, float persistence, float lacunarity)
{
    float total = 0;
    float frequency = 1;
    float amplitude = 1;
    float maxValue = 0; // Used for normalizing result to 0.0 - 1.0

    for (int i = 0; i < octaves; i++)
    {
        total += Mathf.PerlinNoise(x * frequency, y * frequency) * amplitude;

        maxValue += amplitude;

        amplitude *= persistence;
        frequency *= lacunarity;
    }

    return total / maxValue;
}

C# example of a multi-octave Perlin noise function, commonly used in game engines like Unity.

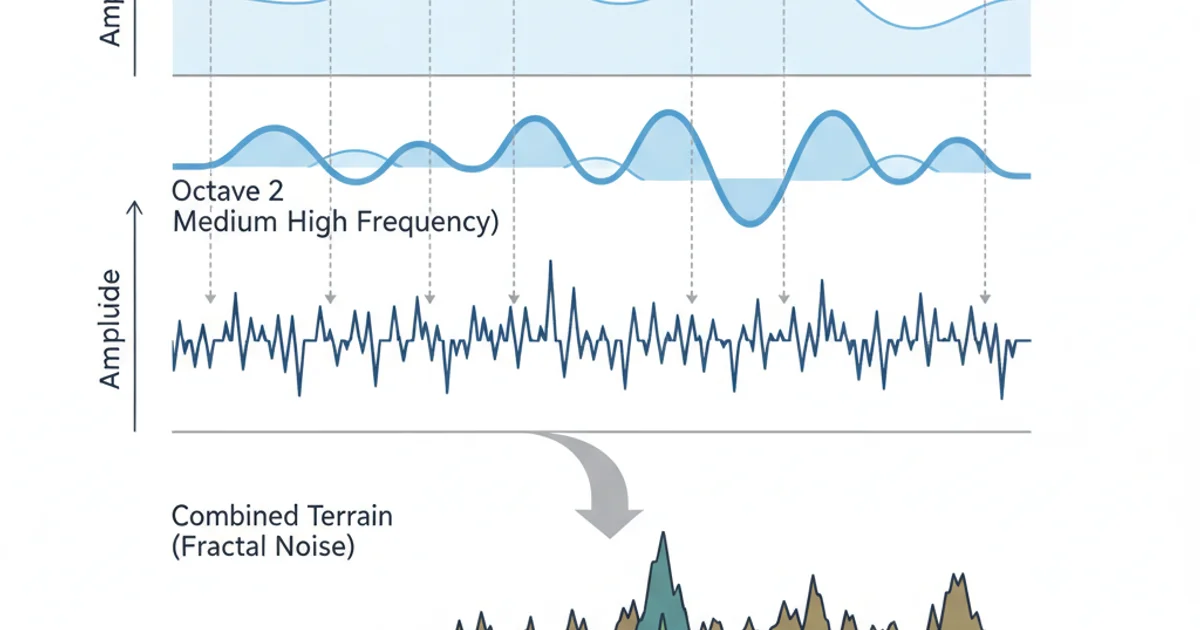
Combining multiple noise octaves to create complex, natural-looking terrain.