What are the differences between NP, NP-Complete and NP-Hard?

Demystifying NP, NP-Complete, and NP-Hard: A Guide to Computational Complexity

Explore the fundamental concepts of computational complexity theory, understanding the distinctions between P, NP, NP-Complete, and NP-Hard problems, and their implications for algorithm design.

In the realm of computer science, understanding the inherent difficulty of problems is crucial for designing efficient algorithms. Computational complexity theory provides a framework for classifying problems based on the resources (time and space) required to solve them. Among the most significant classifications are P, NP, NP-Complete, and NP-Hard. These terms often cause confusion, but grasping their differences is fundamental to appreciating the limits and possibilities of computation. This article will break down each concept, illustrate their relationships, and discuss their practical implications.

The P Class: Polynomial Time Solvable Problems

The class P (Polynomial time) consists of decision problems that can be solved by a deterministic Turing machine in polynomial time. A deterministic Turing machine is a theoretical model of computation that, at any given moment, has at most one possible action for its current state and input symbol. Polynomial time means that the time complexity of the algorithm is bounded by a polynomial function of the input size (e.g., O(n), O(n log n), O(n^2), O(n^3)).

Problems in P are generally considered 'easy' or 'tractable' because their solution time grows relatively slowly with the input size. For practical purposes, if a problem is in P, we can usually find an efficient algorithm to solve it. Examples include sorting a list, searching for an item in a sorted list, or multiplying two numbers.

The NP Class: Nondeterministic Polynomial Time

The class NP (Nondeterministic Polynomial time) consists of decision problems for which a given solution can be verified in polynomial time by a deterministic Turing machine. It's important to note that NP does not stand for 'non-polynomial' or 'not P'. Instead, the 'N' refers to 'nondeterministic'.

For a problem to be in NP, if someone hands you a potential solution, you must be able to check if that solution is correct in polynomial time. The challenge is that finding such a solution might take exponential time. Many problems that are easy to verify are incredibly hard to solve. For instance, if you're given a solution to a Sudoku puzzle, it's quick to check if it's valid. However, finding a solution to an unsolved Sudoku puzzle can be much harder.

All problems in P are also in NP. If you can solve a problem in polynomial time, you can certainly verify a solution in polynomial time (by simply solving it and comparing the result). The big open question in computer science is whether P = NP, meaning whether every problem whose solution can be quickly verified can also be quickly solved. Most computer scientists believe P ≠ NP.

flowchart TD
    P[P: Polynomial Time Solvable] --> NP[NP: Nondeterministic Polynomial Time Verifiable]
    NP --> NPC[NP-Complete: Hardest in NP]
    NPC --> NPH[NP-Hard: At least as hard as NP-Complete]
    NPH --"Includes problems not in NP"--> Other[Other Hard Problems]
    subgraph Relationship
        P --"Subset of"--> NP
        NPC --"Subset of"--> NP
        NPC --"Subset of"--> NPH
    end
    style P fill:#bbf,stroke:#333,stroke-width:2px
    style NP fill:#f9f,stroke:#333,stroke-width:2px
    style NPC fill:#f66,stroke:#333,stroke-width:2px
    style NPH fill:#f00,stroke:#333,stroke-width:2px
    style Other fill:#ccc,stroke:#333,stroke-width:2px

Relationship between P, NP, NP-Complete, and NP-Hard complexity classes.

NP-Complete: The Hardest Problems in NP

NP-Complete (NPC) problems are the 'hardest' problems within the NP class. A decision problem L is NP-Complete if:

1. L is in NP.
2. Every problem in NP can be reduced to L in polynomial time. This means that if you had a polynomial-time algorithm for L, you could use it to solve any other problem in NP in polynomial time.

The concept of 'reduction' is key here. If problem A can be reduced to problem B, it means that an instance of A can be transformed into an instance of B in polynomial time, such that solving the instance of B gives a solution to the instance of A. If you find a polynomial-time algorithm for any NP-Complete problem, then P = NP, and all problems in NP could be solved efficiently.

Examples of NP-Complete problems include the Traveling Salesperson Problem (decision version), the Satisfiability Problem (SAT), the Clique Problem, and the Subset Sum Problem. These problems are notoriously difficult to solve optimally for large inputs, and no polynomial-time algorithms have been found for them despite decades of research.

NP-Hard: At Least as Hard as NP-Complete

NP-Hard problems are a class of problems that are 'at least as hard as' the hardest problems in NP. A problem H is NP-Hard if every problem in NP can be reduced to H in polynomial time. The crucial distinction from NP-Complete is that an NP-Hard problem does not necessarily have to be in NP itself.

This means an NP-Hard problem might not be a decision problem, or its solutions might not be verifiable in polynomial time. For example, the optimization version of the Traveling Salesperson Problem (finding the shortest tour, not just determining if a tour below a certain length exists) is NP-Hard but not NP-Complete, because it's not a decision problem. If you could solve an NP-Hard problem in polynomial time, you could solve all NP-Complete problems in polynomial time.

Many NP-Hard problems are function problems (finding an optimal solution) rather than decision problems (yes/no answers). All NP-Complete problems are also NP-Hard, but not all NP-Hard problems are NP-Complete.

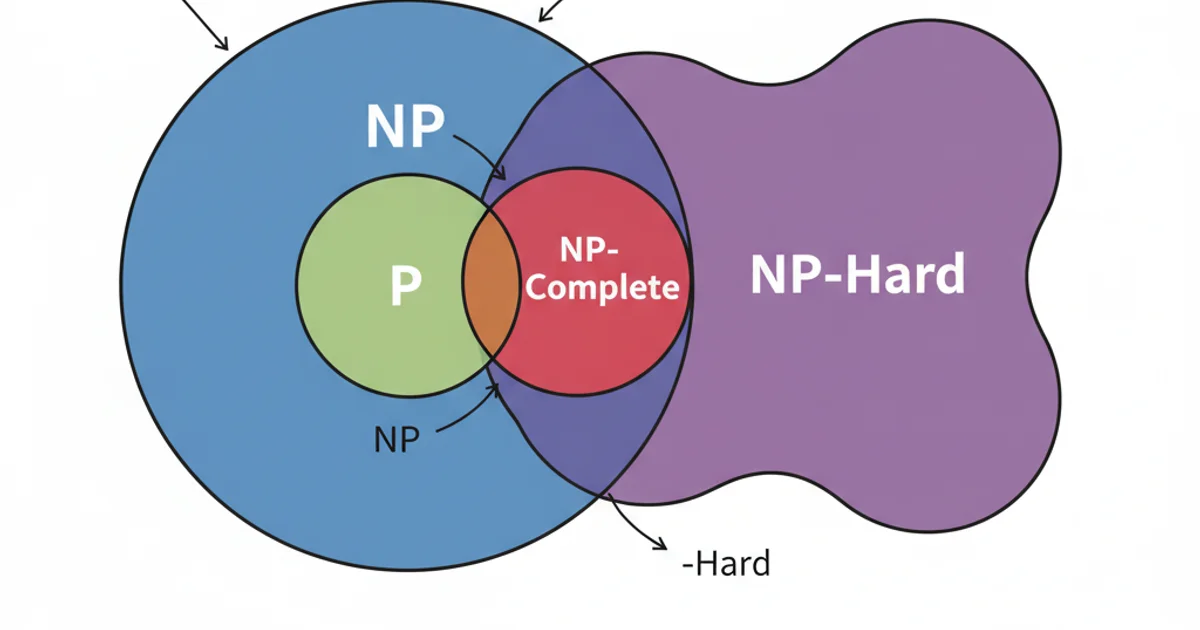
A visual representation of the relationships between the complexity classes.

Understanding these classifications helps computer scientists and developers make informed decisions about algorithm design. When faced with a problem, identifying its complexity class can guide the approach:

• P Problem: Seek an efficient, exact algorithm.
• NP-Complete/NP-Hard Problem: Consider approximation algorithms, heuristics, or specialized exponential algorithms for small instances, as a polynomial-time exact solution is unlikely to exist.