How to think in recursive way?

Mastering Recursion: A Guide to Thinking Recursively

Unlock the power of recursion in programming. This guide demystifies recursive thinking, provides practical examples, and compares it with iterative approaches.

Recursion is a fundamental concept in computer science and programming, often described as a function calling itself. While it can seem intimidating at first, understanding how to think recursively opens up elegant solutions to complex problems that might be cumbersome with iterative approaches. This article will guide you through the core principles of recursion, illustrate its application with practical examples, and help you develop a recursive mindset.

What is Recursion?

At its heart, recursion involves defining a problem in terms of smaller, similar subproblems. A recursive function solves a problem by calling itself with a smaller input until it reaches a base case. The base case is a simple, non-recursive condition that provides a direct solution, preventing infinite loops. Without a properly defined base case, a recursive function will continue calling itself indefinitely, leading to a stack overflow error.

flowchart TD
    A[Start Function Call] --> B{Is Base Case Met?}
    B -- No --> C[Call Function with Smaller Input]
    C --> A
    B -- Yes --> D[Return Base Case Result]
    D --> E[Propagate Result Up]
    E --> F[Final Result]

Flowchart illustrating the recursive process

The Two Pillars of Recursive Thinking

To think recursively, you need to identify two critical components within any problem:

1. The Base Case: This is the simplest instance of the problem that can be solved directly without further recursion. It's the stopping condition.
2. The Recursive Step: This is how you break down the larger problem into a smaller, identical subproblem and combine its solution with the current step to solve the original problem. It's the part where the function calls itself.

Practical Example: Calculating Factorial

Let's consider a classic example: calculating the factorial of a non-negative integer n. The factorial of n (denoted as n!) is the product of all positive integers less than or equal to n. For example, 5! = 5 * 4 * 3 * 2 * 1 = 120. By definition, 0! = 1.

How can we define this recursively?

• Base Case: If n is 0, the factorial is 1.
• Recursive Step: If n is greater than 0, n! = n * (n-1)!. Notice how (n-1)! is a smaller instance of the same problem.

Python

def factorial(n): if n == 0: return 1 # Base case else: return n * factorial(n - 1) # Recursive step

print(factorial(5)) # Output: 120 print(factorial(0)) # Output: 1

JavaScript

function factorial(n) { if (n === 0) { return 1; // Base case } else { return n * factorial(n - 1); // Recursive step } }

console.log(factorial(5)); // Output: 120 console.log(factorial(0)); // Output: 1

Java

public class Factorial { public static int factorial(int n) { if (n == 0) { return 1; // Base case } else { return n * factorial(n - 1); // Recursive step } }

public static void main(String[] args) {
    System.out.println(factorial(5)); // Output: 120
    System.out.println(factorial(0)); // Output: 1
}

}

Recursion vs. Iteration

Many problems solvable with recursion can also be solved iteratively (using loops). While recursion often leads to more concise and readable code for certain problems (like tree traversals or fractal generation), iteration can sometimes be more efficient in terms of memory and performance, as it avoids the overhead of function call stacks.

Tail Recursion: A special form of recursion where the recursive call is the very last operation in the function. Some compilers can optimize tail-recursive functions into iterative code, eliminating stack overflow risks and improving performance. However, not all languages or compilers support this optimization.

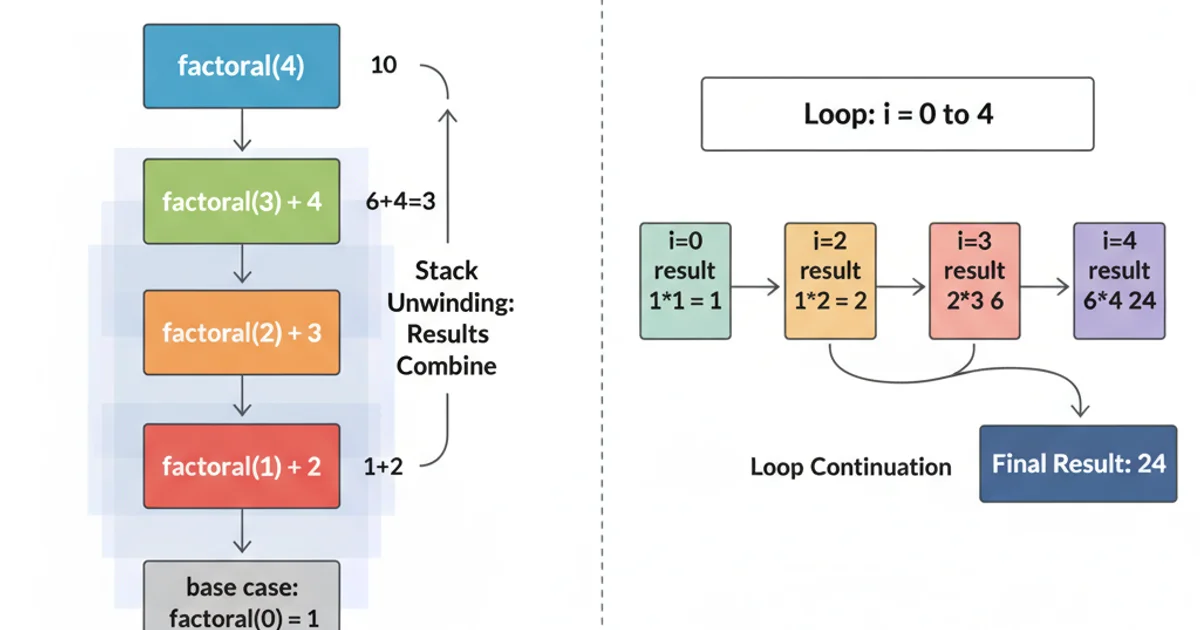
Visualizing the difference between recursive stack calls and iterative loop execution.

def factorial_iterative(n):
    result = 1
    for i in range(1, n + 1):
        result *= i
    return result

print(factorial_iterative(5)) # Output: 120

Iterative approach to calculating factorial in Python

Steps to Think Recursively

To effectively apply recursion, follow these steps:

1. Understand the Problem

Clearly define what the function should do and what its inputs and outputs are. What is the goal?

2. Identify the Base Case

What is the simplest possible input for which you know the answer immediately, without needing further computation? This is your stopping condition.

3. Define the Recursive Step

How can you break the problem down into a smaller instance of the exact same problem? Assume the recursive call works correctly for the smaller problem, and then figure out how to use its result to solve the current problem.

4. Combine and Test

Put the base case and recursive step together. Trace the execution with a small input to ensure it works as expected and reaches the base case.