c# math cos different values from calculator

Understanding C# Math.Cos Discrepancies with Calculators

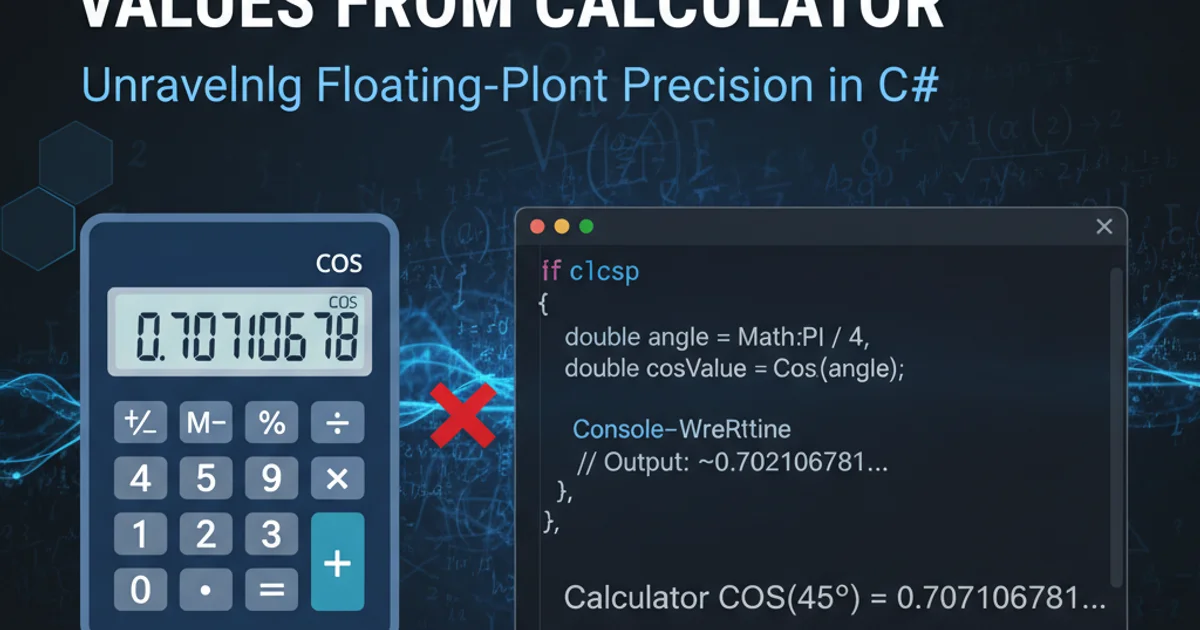
Explore why C#'s Math.Cos function might yield different results than your calculator and how to achieve consistent trigonometric calculations.

Have you ever used Math.Cos in C# and found the result didn't quite match what your scientific calculator showed? This is a common point of confusion for many developers. The discrepancy usually isn't due to a bug in C# or your calculator, but rather a fundamental difference in how angles are interpreted: radians versus degrees.

The Radian vs. Degree Dilemma

Most scientific calculators, by default, operate in degree mode. This means when you input an angle like 90, it interprets it as 90 degrees. However, C#'s Math.Cos (and indeed, most trigonometric functions in programming languages like Java, Python, JavaScript, etc.) expects angles to be in radians. A radian is a unit of angle, where one radian is the angle subtended at the center of a circle by an arc equal in length to the radius. The conversion factor is crucial: π radians = 180 degrees.

flowchart TD
    A[User Inputs Angle] --> B{Calculator Mode?}
    B -->|Degrees| C[Calculator Calculates Cos(Angle in Degrees)]
    B -->|Radians| D[Calculator Calculates Cos(Angle in Radians)]
    A --> E{C# Math.Cos Input?}
    E -->|Expects Radians| F[C# Calculates Cos(Angle in Radians)]
    E -->|Input in Degrees| G["Mismatched Input: Cos(Angle in Degrees) treated as Radians"]
    C --> H{Result}
    D --> H
    F --> H
    G --> I["Unexpected Result (if input was degrees)"]

Flowchart illustrating angle interpretation in calculators vs. C#.

Converting Between Degrees and Radians

To get consistent results, you need to ensure that the angle you pass to Math.Cos is in radians if your original angle is in degrees. The conversion formulas are straightforward:

• Degrees to Radians: radians = degrees * (Math.PI / 180)
• Radians to Degrees: degrees = radians * (180 / Math.PI)

Math.PI in C# provides the value of π (pi), which is approximately 3.14159.

using System;

public class CosineExample
{
    public static void Main(string[] args)
    {
        // Example 1: 90 degrees
        double angleDegrees = 90.0;
        double angleRadians = angleDegrees * (Math.PI / 180.0);

        double cosValueRadians = Math.Cos(angleRadians);
        Console.WriteLine($"Cos({angleDegrees}°): {cosValueRadians} (C# with conversion)");
        // Expected: ~0.0

        double cosValueWithoutConversion = Math.Cos(angleDegrees);
        Console.WriteLine($"Cos({angleDegrees} treated as radians): {cosValueWithoutConversion} (C# without conversion)");
        // Expected: ~-0.448 (incorrect if 90 degrees was intended)

        // Example 2: 0 degrees
        angleDegrees = 0.0;
        angleRadians = angleDegrees * (Math.PI / 180.0);
        cosValueRadians = Math.Cos(angleRadians);
        Console.WriteLine($"\nCos({angleDegrees}°): {cosValueRadians} (C# with conversion)");
        // Expected: 1.0

        // Example 3: 180 degrees
        angleDegrees = 180.0;
        angleRadians = angleDegrees * (Math.PI / 180.0);
        cosValueRadians = Math.Cos(angleRadians);
        Console.WriteLine($"\nCos({angleDegrees}°): {cosValueRadians} (C# with conversion)");
        // Expected: -1.0
    }
}

C# code demonstrating degree-to-radian conversion for Math.Cos.

Precision Considerations

Even with correct unit conversion, you might observe tiny differences (e.g., 1.22E-16 instead of 0). This is due to the nature of floating-point arithmetic in computers. double precision numbers can't perfectly represent all real numbers, leading to minute inaccuracies. For practical purposes, values very close to zero (like 1.22E-16) should be considered zero. If exact comparisons are needed, compare against a small epsilon value rather than direct equality.

using System;

public static class AngleConverter
{
    public static double ToRadians(this double degrees)
    {
        return degrees * (Math.PI / 180.0);
    }

    public static double ToDegrees(this double radians)
    {
        return radians * (180.0 / Math.PI);
    }

    public static void Main(string[] args)
    {
        double angleInDegrees = 90.0;
        double cosResult = Math.Cos(angleInDegrees.ToRadians());
        Console.WriteLine($"Cos({angleInDegrees}°): {cosResult}"); // Output will be very close to 0

        double epsilon = 0.000000000000001; // A small value for comparison
        if (Math.Abs(cosResult) < epsilon)
        {
            Console.WriteLine("Result is effectively zero.");
        }
    }
}

Helper methods for angle conversion and handling floating-point precision.