Java calculator, how to handle negative numbers
Categories:
Mastering Negative Numbers in Java Calculator Implementations

Learn robust techniques for parsing and evaluating expressions with negative numbers in Java-based calculators, covering common pitfalls and effective solutions.
Implementing a calculator in Java often presents challenges beyond basic arithmetic. One common hurdle is correctly handling negative numbers, especially when they appear at the beginning of an expression or immediately after an operator. This article delves into strategies for parsing and evaluating expressions that include negative numbers, ensuring your Java calculator functions accurately and reliably.
The Ambiguity of the Minus Sign
The primary difficulty with negative numbers in a calculator context stems from the dual role of the minus sign (-). It can represent either a subtraction operator or a unary negation (making a number negative). For example, in 5 - 3, it's subtraction. In -3, it's negation. And in 5 * -3, it's also negation. A robust parsing strategy must differentiate between these two uses.
flowchart TD
A[Input Expression] --> B{Is '-' at start or after operator?}
B -- Yes --> C[Treat as Unary Negation]
B -- No --> D[Treat as Subtraction Operator]
C --> E[Parse Number as Negative]
D --> F[Parse as Binary Operation]
E --> G[Evaluate Expression]
F --> GDecision flow for interpreting the minus sign in an expression.
Parsing Strategies for Negative Numbers
Several approaches can be used to correctly parse negative numbers. The most common involve tokenization and operator precedence parsing. We'll explore how to modify these to handle unary minus effectively.
Strategy 1: Token Pre-processing
One effective method is to pre-process the input string to convert unary minus signs into a distinct token or to modify the number itself. For instance, -5 could become (0 - 5) or the token for 5 could be marked as negative.
public class CalculatorParser {
public static List<String> tokenize(String expression) {
List<String> tokens = new ArrayList<>();
// Example: "-5 + 3 * -2"
// Should become: ["-5", "+", "3", "*", "-2"]
// Simple regex to split by operators, but needs refinement for unary minus
Pattern pattern = Pattern.compile("\\d+(\\.\\d+)?|[-+*/()]|(?<=[-+*/(])-\\d+(\\.\\d+)?");
Matcher matcher = pattern.matcher(expression.replaceAll("\\s+", ""));
while (matcher.find()) {
String token = matcher.group();
tokens.add(token);
}
return tokens;
}
// A more robust tokenization might involve iterating character by character
// and building numbers, handling unary minus based on context.
public static List<String> advancedTokenize(String expression) {
List<String> tokens = new ArrayList<>();
String cleanedExpression = expression.replaceAll("\\s+", "");
StringBuilder currentToken = new StringBuilder();
for (int i = 0; i < cleanedExpression.length(); i++) {
char c = cleanedExpression.charAt(i);
if (Character.isDigit(c) || c == '.') {
currentToken.append(c);
} else {
if (currentToken.length() > 0) {
tokens.add(currentToken.toString());
currentToken = new StringBuilder();
}
if (c == '-' && (i == 0 || isOperator(cleanedExpression.charAt(i-1)) || cleanedExpression.charAt(i-1) == '(')) {
// This is likely a unary minus
currentToken.append(c);
} else {
// This is a binary operator
tokens.add(String.valueOf(c));
}
}
}
if (currentToken.length() > 0) {
tokens.add(currentToken.toString());
}
return tokens;
}
private static boolean isOperator(char c) {
return c == '+' || c == '-' || c == '*' || c == '/';
}
}
Example of an advanced tokenization method that distinguishes unary minus.
Strategy 2: Shunting-Yard Algorithm with Unary Minus
The Shunting-Yard algorithm, used to convert infix expressions to Reverse Polish Notation (RPN), can be adapted. When a minus sign is encountered, its context determines if it's a unary operator. If it is, it can be pushed onto the operator stack with a higher precedence than binary minus, or a special 'unary minus' token can be used.
-5 * 2 is correctly interpreted as (-5) * 2 rather than -(5 * 2).Evaluation of RPN with Negative Numbers
Once an expression is converted to RPN (Reverse Polish Notation), evaluation becomes straightforward. When processing the RPN tokens, if you encounter a number, push it onto a stack. If you encounter an operator, pop the required number of operands from the stack, perform the operation, and push the result back. For unary minus, you would pop one operand, negate it, and push it back.
import java.util.Stack;
import java.util.List;
import java.util.ArrayList;
import java.util.regex.Matcher;
import java.util.regex.Pattern;
public class RPNCalculator {
// Assume advancedTokenize from above is available
// and a shuntingYard method to convert tokens to RPN
public static double evaluateRPN(List<String> rpnTokens) {
Stack<Double> stack = new Stack<>();
for (String token : rpnTokens) {
try {
// If it's a number (including negative numbers like "-5")
stack.push(Double.parseDouble(token));
} catch (NumberFormatException e) {
// It's an operator
if (token.equals("~")) { // Assuming '~' is our unary minus operator
double operand = stack.pop();
stack.push(-operand);
} else {
double operand2 = stack.pop();
double operand1 = stack.pop();
switch (token) {
case "+": stack.push(operand1 + operand2); break;
case "-": stack.push(operand1 - operand2); break;
case "*": stack.push(operand1 * operand2); break;
case "/":
if (operand2 == 0) throw new ArithmeticException("Division by zero");
stack.push(operand1 / operand2);
break;
default: throw new IllegalArgumentException("Unknown operator: " + token);
}
}
}
}
return stack.pop();
}
// Example of a simplified Shunting-Yard that handles unary minus
public static List<String> shuntingYard(List<String> tokens) {
List<String> output = new ArrayList<>();
Stack<String> operators = new Stack<>();
// Map operator precedence
Map<String, Integer> precedence = new HashMap<>();
precedence.put("+", 1); precedence.put("-", 1);
precedence.put("*", 2); precedence.put("/", 2);
precedence.put("~", 3); // Unary minus has highest precedence
for (String token : tokens) {
if (token.matches("-?\\d+(\\.\\d+)?")) { // It's a number (possibly negative)
output.add(token);
} else if (token.equals("(")) {
operators.push(token);
} else if (token.equals(")")) {
while (!operators.isEmpty() && !operators.peek().equals("(")) {
output.add(operators.pop());
}
if (!operators.isEmpty() && operators.peek().equals("(")) {
operators.pop(); // Pop '('
} else {
throw new IllegalArgumentException("Mismatched parentheses");
}
} else { // It's an operator
// Special handling for unary minus: if it's a '-' and the previous token was an operator or '(', it's unary.
// For simplicity here, we assume advancedTokenize already converted it to a distinct token like '~'.
String currentOperator = token;
if (token.equals("-") && (output.isEmpty() || isOperator(output.get(output.size()-1).charAt(0)) || output.get(output.size()-1).equals("("))) {
currentOperator = "~"; // Represent unary minus as '~'
}
while (!operators.isEmpty() && !operators.peek().equals("(") &&
precedence.getOrDefault(operators.peek(), 0) >= precedence.getOrDefault(currentOperator, 0)) {
output.add(operators.pop());
}
operators.push(currentOperator);
}
}
while (!operators.isEmpty()) {
if (operators.peek().equals("(")) {
throw new IllegalArgumentException("Mismatched parentheses");
}
output.add(operators.pop());
}
return output;
}
private static boolean isOperator(char c) {
return c == '+' || c == '-' || c == '*' || c == '/';
}
}
RPN evaluation logic and a simplified Shunting-Yard adaptation for unary minus.
double values can lead to inaccuracies. For financial or highly precise calculations, consider using BigDecimal.Testing and Edge Cases
Thorough testing is crucial for any calculator implementation, especially when dealing with negative numbers. Consider the following edge cases:
- Leading negative:
-5 + 3 - Negative after operator:
5 * -3 - Multiple negatives:
-5 - -3(which is-5 + 3) - Parentheses with negatives:
-(5 + 3),5 * (-3 + 2) - Zero and negative zero:
0 - 5,-0.0 - Floating-point negatives:
-3.14 * 2.0
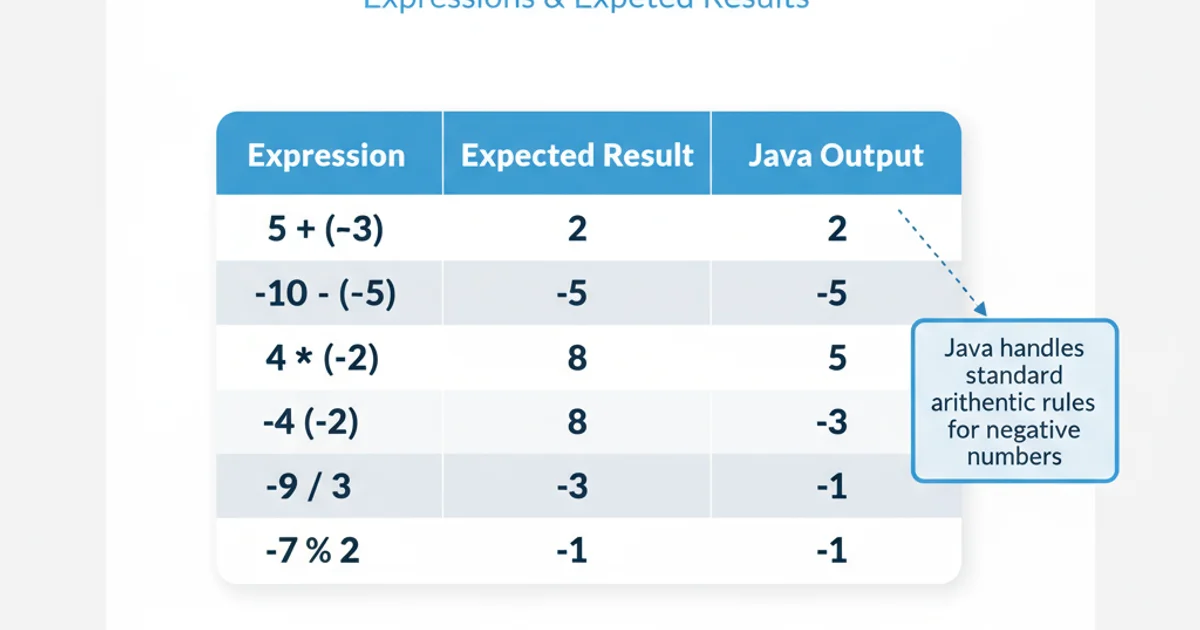
Examples of expressions with negative numbers and their correct evaluations.
By carefully designing your tokenization and parsing logic to differentiate between unary and binary minus, and by rigorously testing against various scenarios, you can build a robust Java calculator capable of handling negative numbers with precision.