how to determine a balanced or perfectly balanced Binary search tree ( just from the picture )

Visual Identification: Balanced vs. Perfectly Balanced Binary Search Trees

Learn to distinguish between balanced and perfectly balanced Binary Search Trees (BSTs) simply by looking at their visual representation, without needing to write code.

Binary Search Trees (BSTs) are fundamental data structures in computer science, offering efficient data retrieval, insertion, and deletion operations. However, their performance heavily relies on their 'balance'. An unbalanced BST can degrade to the performance of a linked list, making operations much slower. This article will guide you through visually identifying balanced and perfectly balanced BSTs, a crucial skill for understanding their efficiency characteristics.

Understanding Tree Balance

Before diving into visual identification, let's define what 'balance' means in the context of a Binary Search Tree. The balance of a tree is generally determined by the height difference between its left and right subtrees. A tree is considered balanced if this height difference is kept within a certain threshold for all nodes. This prevents the tree from becoming skewed and ensures logarithmic time complexity for most operations.

graph TD
    A[Binary Search Tree] --> B{Is it Balanced?}
    B -->|Yes| C[Efficient Operations]
    B -->|No| D[Degraded Performance]
    C --> E{Is it Perfectly Balanced?}
    E -->|Yes| F[Optimal Performance]
    E -->|No| G[Good Performance]

Decision flow for tree balance and performance

What is a Balanced Binary Search Tree?

A Binary Search Tree is considered 'balanced' if, for every node, the height difference between its left and right subtrees is no more than 1. This is the definition used by self-balancing BSTs like AVL trees and Red-Black trees. Visually, a balanced tree will appear relatively 'bushy' or 'spread out', without any single branch extending significantly further down than others. It won't necessarily be symmetrical, but it won't be heavily skewed to one side.

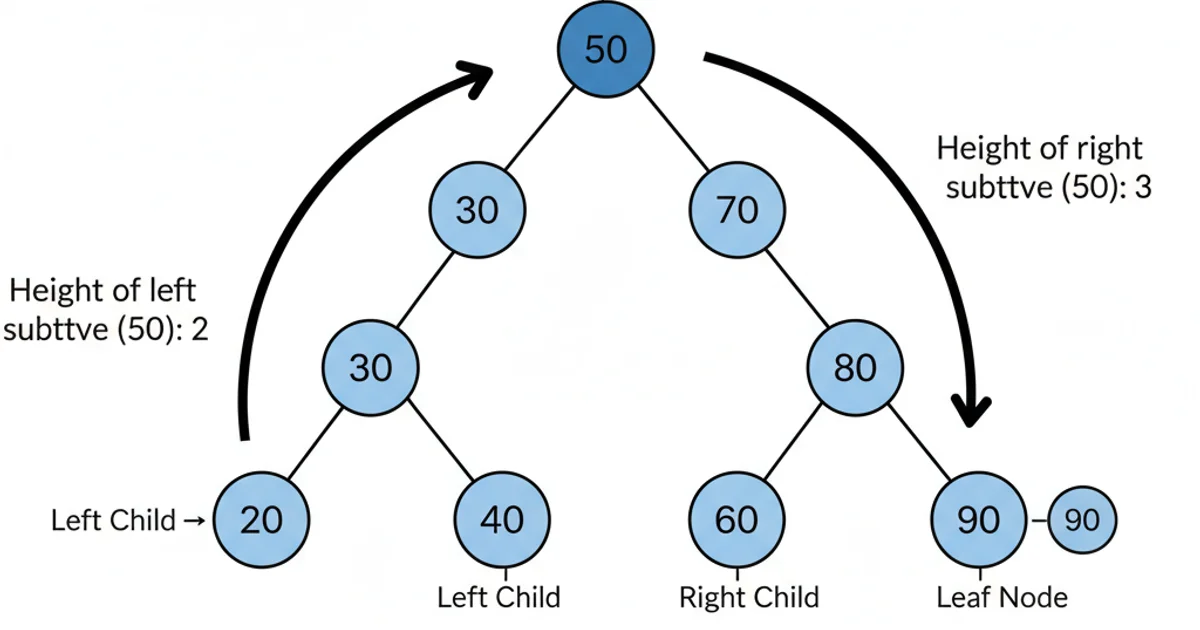
Example of a Balanced Binary Search Tree. Notice the relatively even distribution of nodes, though not perfectly symmetrical.

What is a Perfectly Balanced Binary Search Tree?

A 'perfectly balanced' Binary Search Tree is a more stringent condition. In a perfectly balanced BST, not only is the height difference between left and right subtrees at most 1 for every node, but also, all leaf nodes are at the same level, or at most two levels apart. Furthermore, all levels, except possibly the last, are completely filled. This results in a tree that looks very symmetrical and compact. A complete binary tree is an example of a perfectly balanced tree.

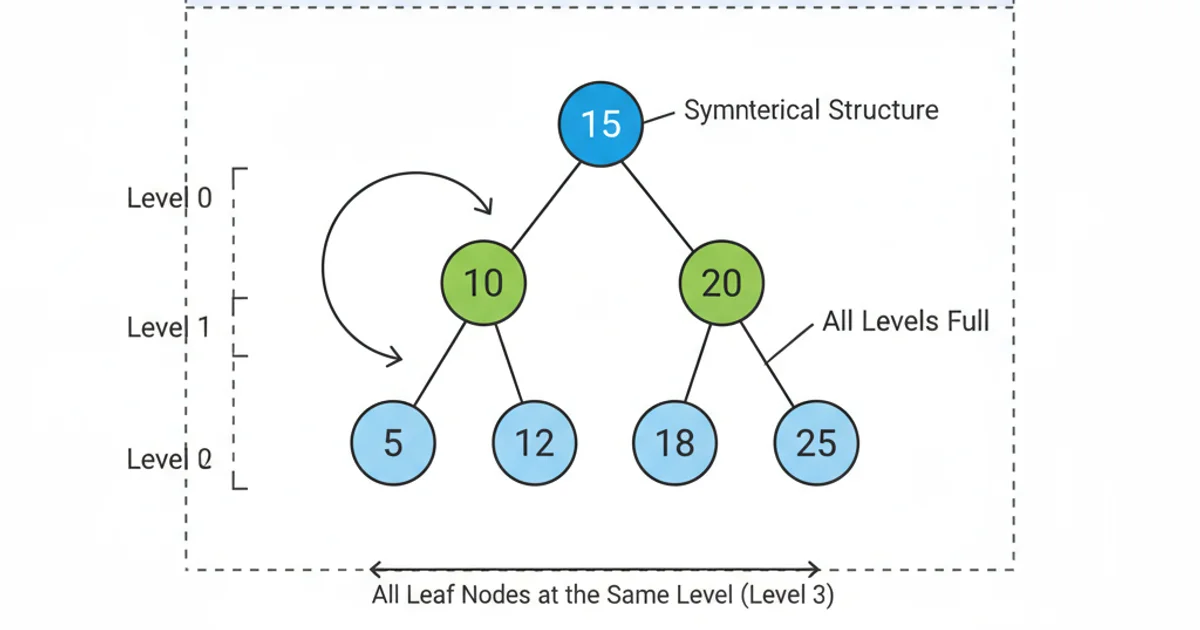
Example of a Perfectly Balanced Binary Search Tree. All levels are full, and leaf nodes are at the same level, creating a highly symmetrical structure.

Visual Comparison and Key Differences

Let's summarize the visual cues to differentiate between these two types of trees:

• Balanced BST: Looks generally 'bushy'. No single path from the root to a leaf is drastically longer than another. The tree doesn't lean heavily to one side. Symmetry is not guaranteed.
• Perfectly Balanced BST: Looks highly symmetrical and compact. All levels are filled, except possibly the last. All leaf nodes are either on the same level or on two adjacent levels. The number of nodes in the left and right subtrees of any node will be very close, often differing by at most one.

graph LR
    A[Unbalanced BST] --> B[Balanced BST]
    B --> C[Perfectly Balanced BST]

    subgraph Characteristics
        A -- "Skewed, long paths" --> A_char
        B -- "Bushy, height diff <= 1" --> B_char
        C -- "Symmetrical, minimal height" --> C_char
    end

Progression from unbalanced to perfectly balanced BSTs and their characteristics

Being able to quickly identify the balance of a BST from a diagram is a valuable skill for debugging, analyzing algorithms, and understanding the theoretical performance implications of different tree structures. While perfectly balanced trees are ideal, they are often hard to maintain during dynamic operations. Balanced trees, maintained by algorithms like AVL or Red-Black trees, strike a practical compromise between optimal performance and ease of maintenance.