Math - how to calculate arccos formula?

Mastering the Arccosine Formula: A Comprehensive Guide

Explore the arccosine function, its mathematical definition, domain, range, and practical applications. Learn how to calculate arccos values using various methods and programming languages.

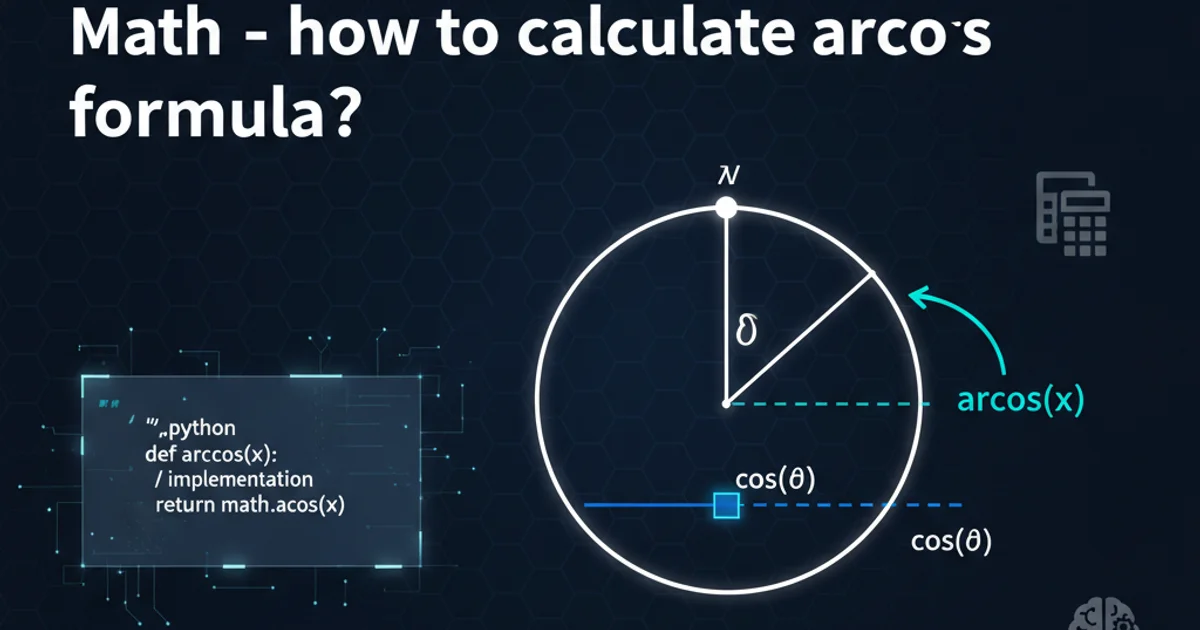
The arccosine function, often denoted as arccos(x) or cos⁻¹(x), is the inverse operation of the cosine function. While the cosine function takes an angle and returns the ratio of the adjacent side to the hypotenuse in a right-angled triangle, arccosine takes this ratio (a value between -1 and 1) and returns the corresponding angle. Understanding arccosine is crucial in various fields, including physics, engineering, computer graphics, and mathematics, for solving problems involving angles and rotations.

Understanding the Arccosine Function

The arccosine function is formally defined as the inverse of the cosine function. For a given value x, y = arccos(x) means that x = cos(y). However, because the cosine function is periodic, it's not one-to-one over its entire domain. To make its inverse a true function, the domain of the cosine function is restricted to [0, π] radians (or [0°, 180°]). This restriction ensures that for every x in the domain [-1, 1], there is a unique angle y in [0, π] such that cos(y) = x.

graph TD
    A[Input: Value x] --> B{Is x in [-1, 1]?}
    B -- Yes --> C[Find angle y such that cos(y) = x]
    C --> D[Ensure y is in [0, π] radians]
    D --> E[Output: Angle y (arccos(x))]
    B -- No --> F[Error: Input out of domain]

Flowchart illustrating the arccosine calculation process and domain restriction.

Calculating Arccosine in Programming Languages

Most programming languages provide built-in functions to calculate arccosine. These functions typically take a floating-point number as input and return the angle in radians. If you need the result in degrees, you'll usually have to convert it manually by multiplying by 180/π.

Python

import math

Example value

x = 0.5

Calculate arccosine in radians

arccos_rad = math.acos(x) print(f"Arccosine of {x} in radians: {arccos_rad}")

Convert to degrees

arccos_deg = math.degrees(arccos_rad) print(f"Arccosine of {x} in degrees: {arccos_deg}")

Example with -1

x_neg = -1 arccos_neg_rad = math.acos(x_neg) print(f"Arccosine of {x_neg} in radians: {arccos_neg_rad}") # Should be pi

JavaScript

// Example value const x = 0.5;

// Calculate arccosine in radians const arccosRad = Math.acos(x); console.log(Arccosine of ${x} in radians: ${arccosRad});

// Convert to degrees const arccosDeg = arccosRad * (180 / Math.PI); console.log(Arccosine of ${x} in degrees: ${arccosDeg});

// Example with -1 const xNeg = -1; const arccosNegRad = Math.acos(xNeg); console.log(Arccosine of ${xNeg} in radians: ${arccosNegRad}); // Should be Math.PI

C++

#include #include

int main() { // Example value double x = 0.5;

// Calculate arccosine in radians
double arccos_rad = std::acos(x);
std::cout << "Arccosine of " << x << " in radians: " << arccos_rad << std::endl;

// Convert to degrees
double arccos_deg = arccos_rad * (180.0 / M_PI);
std::cout << "Arccosine of " << x << " in degrees: " << arccos_deg << std::endl;

// Example with -1
double x_neg = -1.0;
double arccos_neg_rad = std::acos(x_neg);
std::cout << "Arccosine of " << x_neg << " in radians: " << arccos_neg_rad << std::endl; // Should be M_PI

return 0;

}

Common Pitfalls and Considerations

When working with arccosine, it's essential to be aware of potential issues:

1. Domain Errors: Input values outside the [-1, 1] range will result in a domain error or NaN (Not a Number) in most programming environments. Always validate your input if it's user-provided or derived from calculations that might exceed this range.
2. Units: The output is almost universally in radians. If your application requires degrees, remember to perform the conversion.
3. Floating-Point Precision: Due to the nature of floating-point arithmetic, results might not be perfectly exact. Small discrepancies are normal.
4. Quadrant Ambiguity: While arccos itself resolves ambiguity by restricting its range to [0, π], in more complex trigonometric problems, you might need to use atan2 (arctangent of y/x) if you have both x and y components, as atan2 can determine the angle in all four quadrants.