De Morgan's Law

Understanding De Morgan's Laws in Boolean Logic and Programming

Explore De Morgan's Laws, fundamental principles in boolean algebra, and learn how to apply them to simplify complex logical expressions in Java and other programming languages.

De Morgan's Laws are a pair of transformation rules in boolean algebra that are crucial for simplifying logical expressions and understanding the relationships between conjunctions (AND), disjunctions (OR), and negations (NOT). Named after Augustus De Morgan, these laws provide a systematic way to rewrite logical statements, which is incredibly useful in programming, digital circuit design, and formal logic. This article will delve into the two primary laws, demonstrate their application with truth tables, and provide practical examples in Java.

The Two Laws of De Morgan

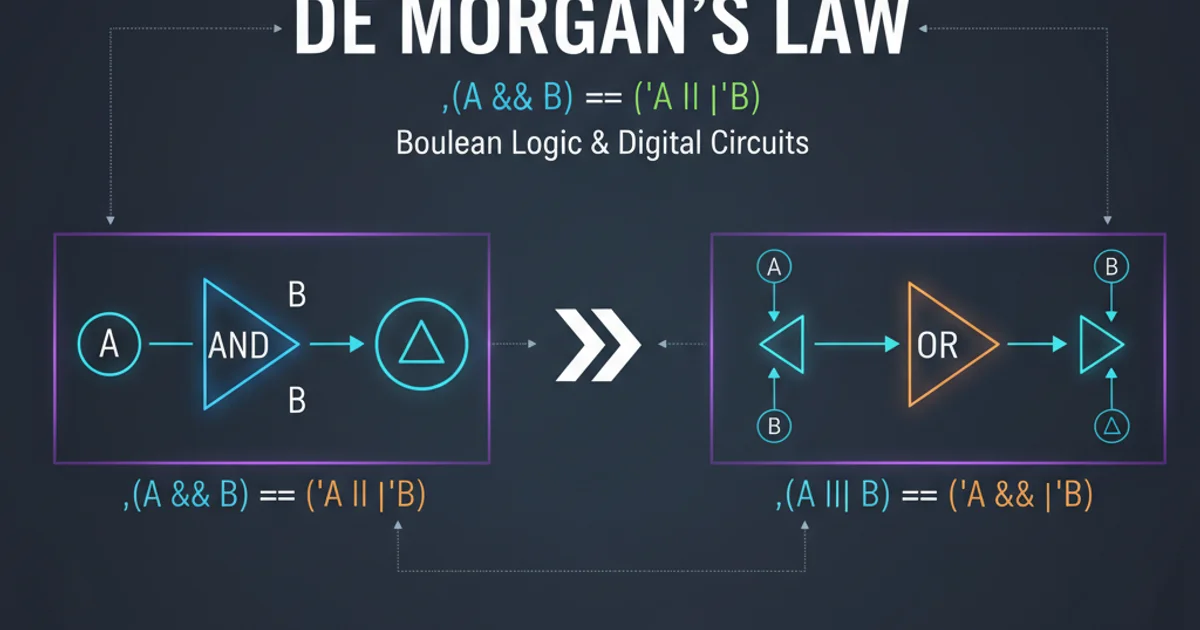
De Morgan's Laws state that the negation of a conjunction is the disjunction of the negations, and the negation of a disjunction is the conjunction of the negations. In simpler terms, they describe how to distribute a negation operator over an AND or an OR operation.

First Law: The negation of (A AND B) is equivalent to (NOT A OR NOT B). Mathematically: NOT (A AND B) <=> (NOT A OR NOT B)

Second Law: The negation of (A OR B) is equivalent to (NOT A AND NOT B). Mathematically: NOT (A OR B) <=> (NOT A AND NOT B)

flowchart LR
    subgraph First Law
        A["NOT (A AND B)"] --> B["NOT A OR NOT B"]
    end
    subgraph Second Law
        C["NOT (A OR B)"] --> D["NOT A AND NOT B"]
    end

Visual representation of De Morgan's Laws

Truth Tables and Verification

Truth tables provide a clear way to verify the equivalence of logical expressions. By evaluating all possible combinations of truth values for the variables, we can confirm that both sides of De Morgan's equations always yield the same result.

First Law: NOT (A AND B) <=> (NOT A OR NOT B)

Truth Table for De Morgan's First Law

Second Law: NOT (A OR B) <=> (NOT A AND NOT B)

Truth Table for De Morgan's Second Law

Practical Application in Java

De Morgan's Laws are incredibly useful in programming for simplifying complex conditional statements, making code more readable, and sometimes optimizing performance. They allow you to convert a condition that checks for the absence of a combined state into a condition that checks for the presence of individual negated states, and vice-versa.

public class DeMorgansLawExample {

    public static void main(String[] args) {
        boolean a = true;
        boolean b = false;

        // First Law: NOT (A AND B) <=> (NOT A OR NOT B)
        boolean not_a_and_b = !(a && b);
        boolean not_a_or_not_b = (!a || !b);
        System.out.println("First Law Verification:");
        System.out.println("!(a && b) = " + not_a_and_b); // Expected: true
        System.out.println("!a || !b = " + not_a_or_not_b); // Expected: true
        System.out.println("Are they equal? " + (not_a_and_b == not_a_or_not_b)); // Expected: true

        System.out.println("\n--------------------\n");

        // Second Law: NOT (A OR B) <=> (NOT A AND NOT B)
        boolean not_a_or_b = !(a || b);
        boolean not_a_and_not_b = (!a && !b);
        System.out.println("Second Law Verification:");
        System.out.println("!(a || b) = " + not_a_or_b); // Expected: false
        System.out.println("!a && !b = " + not_a_and_not_b); // Expected: false
        System.out.println("Are they equal? " + (not_a_or_b == not_a_and_not_b)); // Expected: true
    }
}

Java code demonstrating the equivalence of De Morgan's Laws.

Simplifying Conditional Logic

Let's consider a common scenario where De Morgan's Laws can simplify code. Imagine you have a condition that checks if a user is not both an administrator AND active. Without De Morgan's, it might look like this:

boolean isAdmin = false;
boolean isActive = true;

if (!(isAdmin && isActive)) {
    System.out.println("User is not an active administrator.");
}

Original complex condition.

Applying De Morgan's First Law !(A && B) <=> (!A || !B), we can rewrite the condition as !isAdmin || !isActive:

boolean isAdmin = false;
boolean isActive = true;

if (!isAdmin || !isActive) {
    System.out.println("User is not an active administrator (simplified).");
}

Simplified condition using De Morgan's Law.

The simplified version is often easier to read and understand, as it directly states that the user is either not an administrator OR not active. This clarity is invaluable in maintaining large codebases.