Absolute Value of a Vector in MATLAB

Calculating the Absolute Value (Magnitude) of a Vector in MATLAB

Learn how to effectively compute the absolute value or magnitude of vectors in MATLAB using various built-in functions and understanding their nuances.

In MATLAB, the 'absolute value' of a vector typically refers to its magnitude or Euclidean norm. This is a scalar value representing the length of the vector from the origin to its endpoint. Understanding how to calculate this is fundamental for many mathematical and engineering applications, including signal processing, linear algebra, and physics simulations. This article will guide you through the primary methods for achieving this in MATLAB.

Understanding Vector Magnitude

For a vector ( \mathbf{v} = [v_1, v_2, \dots, v_n] ), its magnitude (or Euclidean norm, denoted as ( ||\mathbf{v}|| ) or ( |\mathbf{v}| )) is calculated as the square root of the sum of the squares of its components. Mathematically, this is expressed as:

( ||\mathbf{v}|| = \sqrt{v_1^2 + v_2^2 + \dots + v_n^2} )

MATLAB provides several convenient functions to perform this calculation efficiently, avoiding the need for manual component-wise operations.

flowchart TD
    A[Start] --> B{Input Vector `v`}
    B --> C["Square each component: `v_i^2`"]
    C --> D["Sum the squared components: `sum(v_i^2)`"]
    D --> E["Take square root: `sqrt(sum(v_i^2))`"]
    E --> F[Output Magnitude `||v||`]
    F --> G[End]

Flowchart for calculating vector magnitude

Using the norm Function

The most direct and recommended way to calculate the magnitude of a vector in MATLAB is by using the norm function. This function is specifically designed for calculating vector and matrix norms, and by default, for a vector, it computes the 2-norm (Euclidean norm), which is precisely the magnitude.

% Define a 2D vector
v2d = [3, 4];

% Calculate its magnitude
magnitude2d = norm(v2d);
disp(['Magnitude of 2D vector: ', num2str(magnitude2d)]);

% Define a 3D vector
v3d = [1, 2, 2];

% Calculate its magnitude
magnitude3d = norm(v3d);
disp(['Magnitude of 3D vector: ', num2str(magnitude3d)]);

Calculating vector magnitude using norm

Alternative: Manual Calculation with sqrt and sum

While norm is the most convenient, you can also compute the magnitude manually by applying the mathematical definition using MATLAB's element-wise operations and functions like sqrt and sum. This method can be useful for understanding the underlying calculation or in scenarios where you might be building custom functions.

% Define a vector
v = [5, -12, 0];

% Square each element
squared_elements = v.^2;

% Sum the squared elements
sum_of_squares = sum(squared_elements);

% Take the square root
manual_magnitude = sqrt(sum_of_squares);
disp(['Manual magnitude calculation: ', num2str(manual_magnitude)]);

Manual calculation of vector magnitude

The abs Function for Element-wise Absolute Value and Complex Modulus

The abs function in MATLAB computes the absolute value of each element in an array. For real numbers, this is straightforward. For complex numbers, abs computes the modulus (magnitude) of each complex number. If you have a vector of complex numbers and you want the magnitude of each individual complex number within that vector, abs is the correct function to use. However, if you want the magnitude of the vector itself (i.e., its Euclidean length in a higher-dimensional space), norm is still the appropriate choice.

% Vector of real numbers
real_vec = [-5, 10, -3.5];
abs_real_vec = abs(real_vec);
disp('Absolute values of real vector elements:');
disp(abs_real_vec);

% Vector of complex numbers
complex_vec = [3 + 4i, -2 - 1i, 0 + 5i];
abs_complex_vec = abs(complex_vec);
disp('Modulus of complex vector elements:');
disp(abs_complex_vec);

% Note: abs(vector) is NOT the vector's magnitude (Euclidean norm)
% For vector magnitude, use norm():
vector_magnitude = norm(complex_vec);
disp(['Magnitude (Euclidean norm) of complex vector: ', num2str(vector_magnitude)]);

Using abs for element-wise absolute value and complex modulus

Summary of Functions

Here's a quick recap of the functions discussed and their primary use cases for vector magnitudes in MATLAB:

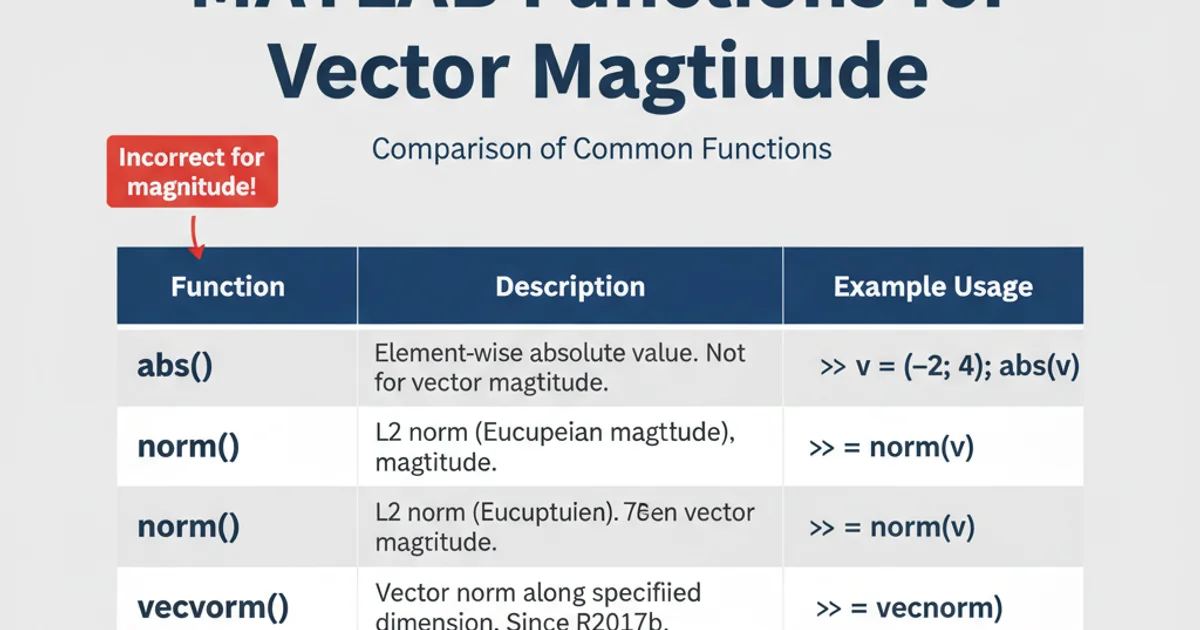
Comparison of MATLAB functions for vector magnitude

1. Choose the Right Function

For the Euclidean magnitude (length) of a vector, always prefer norm(vector). It's robust and efficient.

2. Use abs for Element-wise Operations

If you need the absolute value of each real element or the modulus of each complex element within a vector, use abs(vector).

3. Consider Manual Calculation for Learning

The manual method sqrt(sum(vector.^2)) is good for understanding the concept but less efficient and potentially error-prone for complex numbers compared to norm.