Assembly fast division by 2

Optimizing Division by Two in Assembly Language

Explore efficient methods for dividing integers by two in assembly language, leveraging bitwise operations for performance gains over traditional division instructions.

Dividing a number by two is a fundamental operation in computer programming. While high-level languages often abstract this with a simple / 2 operator, understanding how this is achieved at the assembly level can reveal significant performance optimizations. This article delves into various assembly techniques for fast division by two, focusing on bitwise shifts and their implications for signed and unsigned integers.

Unsigned Integer Division by Two

For unsigned integers, division by two is straightforward and highly efficient using a right bit shift. Each right shift operation effectively divides the number by two, discarding any fractional part (which is always zero for even numbers and 0.5 for odd numbers, meaning the result is always floored). This is because a right shift moves all bits one position to the right, effectively halving the value represented by the binary string.

MOV EAX, 10 ; EAX = 00001010b (10 decimal)
SHR EAX, 1  ; EAX = 00000101b (5 decimal)

MOV EBX, 11 ; EBX = 00001011b (11 decimal)
SHR EBX, 1  ; EBX = 00000101b (5 decimal)

Example of SHR (Shift Right) for unsigned division by two.

Signed Integer Division by Two

Dividing signed integers by two using bit shifts is more nuanced due to how negative numbers are represented (typically two's complement). A simple logical right shift (SHR) would treat the sign bit as a data bit, leading to incorrect results for negative numbers. For signed division, an arithmetic right shift (SAR) is required. The SAR instruction preserves the sign bit by propagating it to the right, ensuring that negative numbers remain negative and are correctly divided.

MOV EAX, 10  ; EAX = 00000000 00000000 00000000 00001010b (10 decimal)
SAR EAX, 1   ; EAX = 00000000 00000000 00000000 00000101b (5 decimal)

MOV EBX, -10 ; EBX = 11111111 11111111 11111111 11110110b (-10 decimal)
SAR EBX, 1   ; EBX = 11111111 11111111 11111111 11111011b (-5 decimal)

MOV ECX, -11 ; ECX = 11111111 11111111 11111111 11110101b (-11 decimal)
SAR ECX, 1   ; ECX = 11111111 11111111 11111111 11111010b (-6 decimal)

Example of SAR (Shift Arithmetic Right) for signed division by two.

flowchart TD
    A[Start]
    A --> B{Is number signed?}
    B -->|No| C[Use SHR instruction]
    B -->|Yes| D{Is number negative and odd?}
    D -->|No| E[Use SAR instruction]
    D -->|Yes| F["SAR will floor (e.g., -11/2 = -6)"]
    C --> G[Result is N/2]
    E --> G
    F --> G

Decision flow for choosing the correct division by two instruction.

Comparison with DIV Instruction

While bit shifts are excellent for division by powers of two, general-purpose division instructions like DIV (for unsigned) or IDIV (for signed) are much more complex and computationally expensive. They are designed to handle division by arbitrary numbers, not just powers of two. Using SHR or SAR when dividing by two offers a significant performance advantage, often executing in a single clock cycle compared to many cycles for DIV/IDIV.

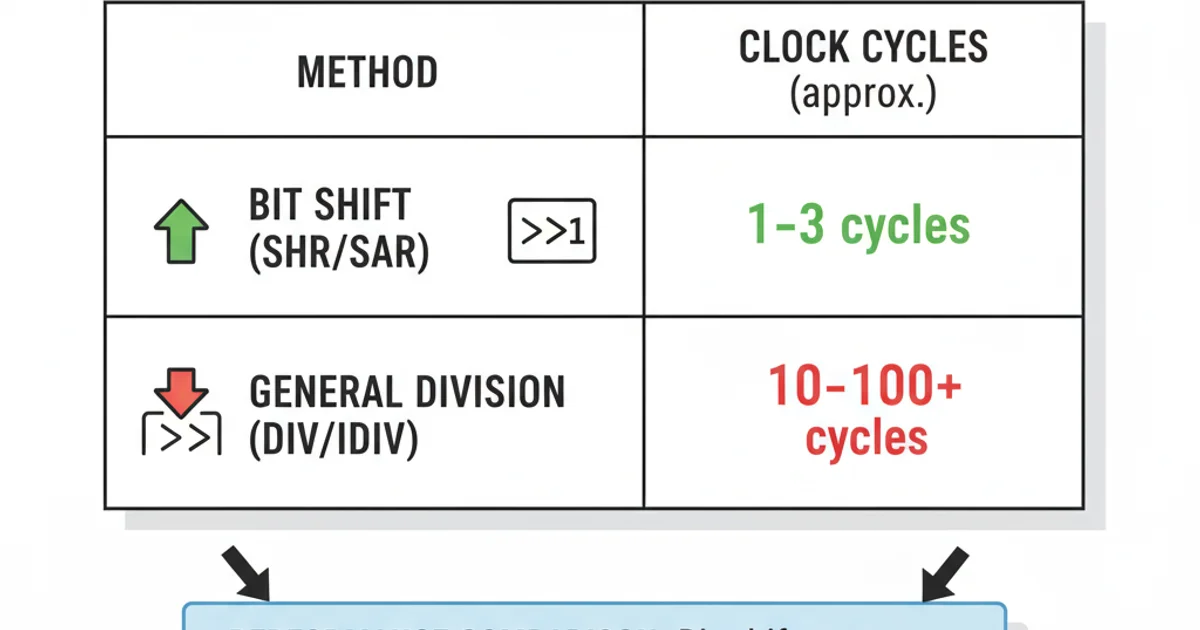
Performance comparison: Bit shifts are significantly faster than general division instructions.