Find radius and position of circle who's curve bases on two points

Calculating Circle Parameters from Two Points and a Curve

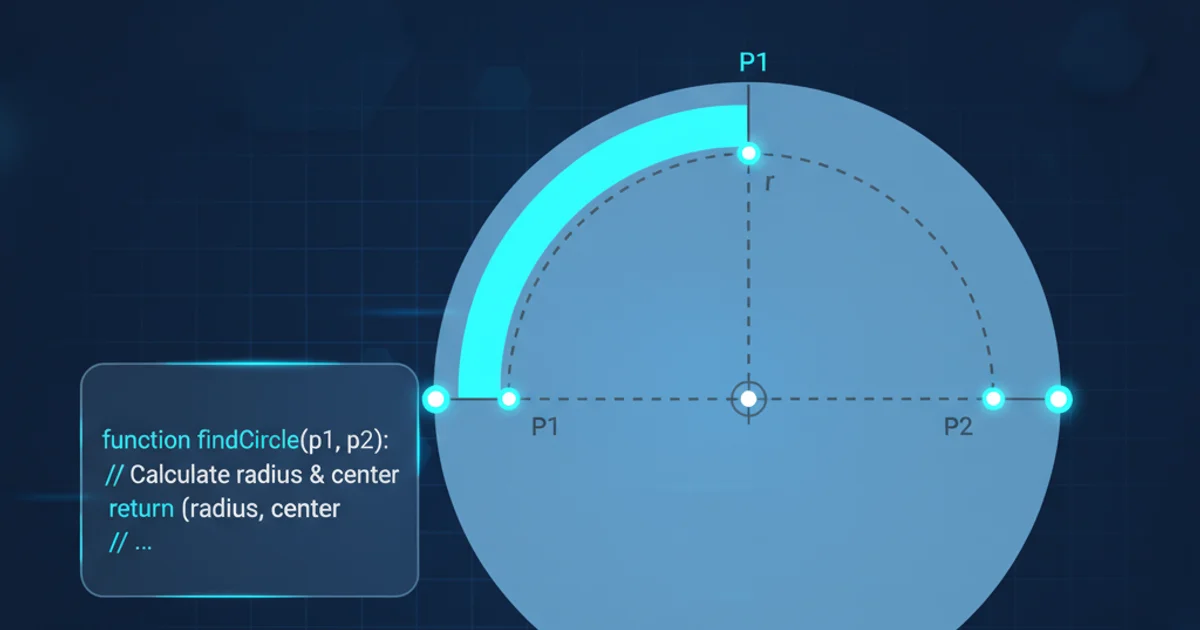
Discover the geometric principles and mathematical formulas to determine the radius and center of a circle whose arc passes through two given points.

Finding the radius and position of a circle when only two points on its circumference are known, and its curve is implied, is a common problem in geometry and various engineering applications. This scenario often arises when you need to reconstruct a circular path from limited data, such as in CAD systems, robotics, or even game development. While two points alone define an infinite number of circles, the 'curve' aspect implies that we are looking for a specific arc that connects these points. This article will guide you through the mathematical approach to solve this problem, focusing on the core geometric relationships.

Understanding the Geometric Constraints

When a circle's curve is based on two points, P1(x1, y1) and P2(x2, y2), these points lie on the circumference of the circle. The line segment connecting P1 and P2 is a chord of the circle. The perpendicular bisector of this chord will always pass through the center of the circle. This is a fundamental geometric property that forms the basis of our solution. However, with only two points, we still have an infinite number of circles whose arcs pass through them. To uniquely define a circle, we typically need a third point, or additional information such as the radius, the center coordinates, or the angle subtended by the arc.

flowchart TD
    A[Start with P1(x1, y1) and P2(x2, y2)] --> B{Calculate Midpoint M of P1P2}
    B --> C{Calculate Slope of P1P2}
    C --> D{Calculate Perpendicular Slope}
    D --> E{Equation of Perpendicular Bisector}
    E --> F{Additional Constraint Needed?}
    F -- Yes --> G[e.g., Radius R, Center (Cx, Cy), or Arc Angle]
    F -- No --> H[Infinite Circles Possible]
    G --> I{Solve for Circle Center (Cx, Cy)}
    I --> J{Verify with Radius R}
    J --> K[End]

Flowchart for determining circle parameters from two points.

The Role of Additional Information

As mentioned, two points are insufficient to define a unique circle. The phrase 'who's curve bases on two points' implies that there's an intended arc. This usually means one of the following is also known:

1. The Radius (R): If the radius is known, we can find two possible centers for the circle.
2. The Center Coordinates (Cx, Cy): If the center is known, the radius is simply the distance from the center to either point.
3. The Arc Angle or Direction: Knowing whether the arc is 'above' or 'below' the chord, or the angle it subtends, can help select between multiple solutions or imply a specific radius.

For the purpose of this article, we will assume the radius R is also provided, as this is a common and practical scenario for uniquely defining the circle.

Mathematical Derivation with Known Radius

Let the two given points be P1(x1, y1) and P2(x2, y2), and the known radius be R. Let the center of the circle be C(Cx, Cy).

1. Midpoint (M) of the Chord P1P2: Mx = (x1 + x2) / 2 My = (y1 + y2) / 2

2. Distance (d) between P1 and P2: d = sqrt((x2 - x1)^2 + (y2 - y1)^2)

3. Distance from Midpoint to Center (h): The chord P1P2 and the radius R form a right-angled triangle with the distance h from the midpoint M to the center C. Using the Pythagorean theorem: R^2 = (d/2)^2 + h^2 h = sqrt(R^2 - (d/2)^2) Note: If R < d/2, then no such circle exists, as the radius is too small to span the chord.

4. Slope of the Chord P1P2 (m_chord): m_chord = (y2 - y1) / (x2 - x1) (Handle vertical chord case where x1 = x2)

5. Slope of the Perpendicular Bisector (m_perp): m_perp = -1 / m_chord (Handle horizontal chord case where y1 = y2)

6. Direction Vector of the Perpendicular Bisector: A unit vector along the perpendicular bisector can be found. If m_chord = (y2-y1)/(x2-x1), then a vector along the chord is (x2-x1, y2-y1). A perpendicular vector is (-(y2-y1), (x2-x1)) or ((y2-y1), -(x2-x1)). Normalize this vector to get (Vx, Vy).

7. Center Coordinates (Cx, Cy): The center C(Cx, Cy) will be at a distance h from the midpoint M along the perpendicular bisector. There will be two possible solutions, one on each side of the chord: Cx = Mx ± h * Vx Cy = My ± h * Vy

   Where (Vx, Vy) is the normalized perpendicular vector. For example, if dx = x2 - x1 and dy = y2 - y1: len_perp_vec = sqrt(dx^2 + dy^2) Vx = -dy / len_perp_vec Vy = dx / len_perp_vec

   Then the two possible centers are: C1x = Mx + h * Vx C1y = My + h * Vy

   C2x = Mx - h * Vx C2y = My - h * Vy

   The choice between C1 and C2 depends on the implied 'curve' direction or additional context.

import math

def find_circle_center_and_radius(p1, p2, R):
    """
    Calculates the center(s) of a circle given two points on its circumference
    and the radius.

    Args:
        p1 (tuple): (x1, y1) - First point.
        p2 (tuple): (x2, y2) - Second point.
        R (float): The radius of the circle.

    Returns:
        list: A list of possible circle centers [(Cx, Cy)].
              Returns an empty list if no solution exists.
    """
    x1, y1 = p1
    x2, y2 = p2

    # 1. Midpoint of the chord P1P2
    Mx = (x1 + x2) / 2
    My = (y1 + y2) / 2

    # 2. Distance between P1 and P2 (chord length)
    d_squared = (x2 - x1)**2 + (y2 - y1)**2
    d = math.sqrt(d_squared)

    # Check if radius is too small
    if R < d / 2:
        print(f"Error: Radius {R} is too small for chord length {d}.")
        return []

    # 3. Distance from Midpoint to Center (h)
    h = math.sqrt(R**2 - (d/2)**2)

    # 4. Direction vector of the chord
    dx = x2 - x1
    dy = y2 - y1

    # 5. Perpendicular direction vector (normalized)
    # (dy, -dx) or (-dy, dx) are perpendicular to (dx, dy)
    # We normalize it to get a unit vector
    len_perp_vec = math.sqrt(dx**2 + dy**2) # This is 'd'
    if len_perp_vec == 0: # Points are identical
        print("Error: Points are identical.")
        return []

    # Unit vector perpendicular to the chord
    # We use (-dy, dx) for one direction, (dy, -dx) for the other
    Vx = -dy / len_perp_vec
    Vy = dx / len_perp_vec

    # 6. Center Coordinates (two possible solutions)
    centers = []
    # First possible center
    C1x = Mx + h * Vx
    C1y = My + h * Vy
    centers.append((C1x, C1y))

    # Second possible center
    C2x = Mx - h * Vx
    C2y = My - h * Vy
    centers.append((C2x, C2y))

    return centers

# Example Usage:
p1 = (0, 0)
p2 = (4, 0)
R = 2.5

possible_centers = find_circle_center_and_radius(p1, p2, R)

if possible_centers:
    print(f"Points: {p1}, {p2}")
    print(f"Radius: {R}")
    for i, center in enumerate(possible_centers):
        print(f"Possible Center {i+1}: ({center[0]:.2f}, {center[1]:.2f})")
else:
    print("No valid circle found with the given parameters.")

# Example 2: Vertical chord
p1_v = (1, 0)
p2_v = (1, 6)
R_v = 5
possible_centers_v = find_circle_center_and_radius(p1_v, p2_v, R_v)
if possible_centers_v:
    print(f"\nPoints: {p1_v}, {p2_v}")
    print(f"Radius: {R_v}")
    for i, center in enumerate(possible_centers_v):
        print(f"Possible Center {i+1}: ({center[0]:.2f}, {center[1]:.2f})")

# Example 3: Radius too small
p1_bad = (0, 0)
p2_bad = (10, 0)
R_bad = 4
find_circle_center_and_radius(p1_bad, p2_bad, R_bad)

Python implementation to find circle centers given two points and a radius.

1. Define Your Inputs

Clearly identify your two points P1(x1, y1) and P2(x2, y2), and the known radius R. Ensure R is positive.

2. Calculate Midpoint and Chord Length

Compute the midpoint M of the segment P1P2 and the total length of the chord d. This is crucial for subsequent calculations.

3. Determine Distance from Midpoint to Center

Use the Pythagorean theorem to find h, the distance from the midpoint M to the circle's center C. Validate that R >= d/2 to ensure a real solution exists.

4. Find Perpendicular Direction Vector

Calculate a unit vector that is perpendicular to the chord P1P2. This vector will point from the midpoint M towards the possible circle centers.

5. Compute Possible Center Coordinates

Add and subtract h times the perpendicular unit vector from the midpoint M's coordinates to find the two potential circle centers. Select the appropriate center based on any additional context about the curve's direction.