How to draw complement of a network graph?

How to Draw the Complement of a Network Graph in Python

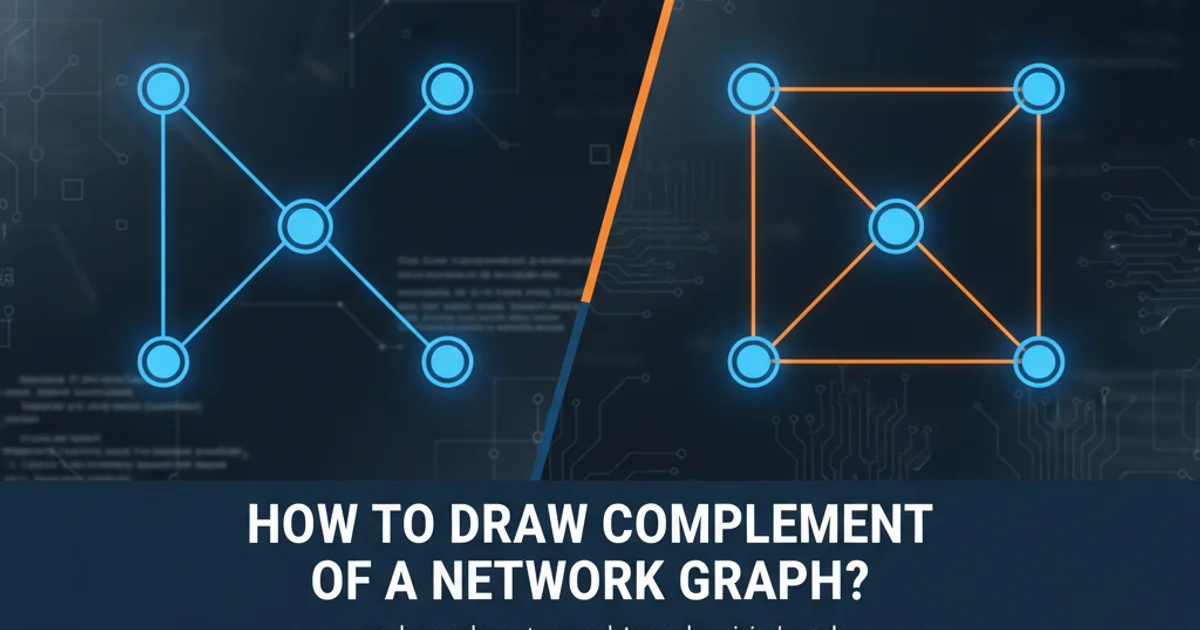
Learn to compute and visualize the complement of a graph using NetworkX and Matplotlib in Python, a fundamental concept in graph theory.

In graph theory, the complement of a graph G is a graph G' on the same vertices such that two distinct vertices are adjacent in G' if and only if they are not adjacent in G. In simpler terms, if there's an edge between two nodes in the original graph, there isn't one in the complement, and vice-versa. Understanding and visualizing graph complements is crucial for various applications, including network analysis, algorithm design, and understanding structural properties of networks. This article will guide you through the process of computing and drawing graph complements using Python's powerful NetworkX library.

Understanding Graph Complements

A graph G is defined by a set of vertices V and a set of edges E. Its complement, denoted as Ḡ (or G'), has the same set of vertices V, but its edge set Ē consists of all possible edges between distinct vertices that are not present in E. This means that if an edge (u, v) exists in G, it does not exist in Ḡ, and if (u, v) does not exist in G, it must exist in Ḡ. Self-loops (edges from a vertex to itself) are typically not considered in this definition.

graph TD
    subgraph Original Graph G
        A -- Edge 1 --> B
        B -- Edge 2 --> C
        C -- Edge 3 --> A
    end

    subgraph Complement Graph G'
        A -- No Edge 1 --> B
        B -- No Edge 2 --> C
        C -- No Edge 3 --> A
    end

    style Original Graph G fill:#f9f,stroke:#333,stroke-width:2px
    style Complement Graph G' fill:#ccf,stroke:#333,stroke-width:2px

    A -- "Original Edge (A,B)" --> B
    B -- "Original Edge (B,C)" --> C
    C -- "Original Edge (C,A)" --> A

    A --- "Complement Edge (A,C)" --- C
    B --- "Complement Edge (B,A)" --- A
    C --- "Complement Edge (C,B)" --- B

    linkStyle 0 stroke-dasharray: 5 5
    linkStyle 1 stroke-dasharray: 5 5
    linkStyle 2 stroke-dasharray: 5 5
    linkStyle 3 stroke:#f00,stroke-width:2px
    linkStyle 4 stroke:#f00,stroke-width:2px
    linkStyle 5 stroke:#f00,stroke-width:2px

Conceptual illustration of a graph and its complement. Dashed lines represent original edges, solid red lines represent complement edges.

Implementing Graph Complement with NetworkX

NetworkX is a Python library for the creation, manipulation, and study of the structure, dynamics, and functions of complex networks. It provides a straightforward function to compute the complement of a graph. We'll demonstrate this with a simple example, creating a small graph, finding its complement, and then visualizing both.

import networkx as nx
import matplotlib.pyplot as plt

# 1. Create an original graph
G = nx.Graph()
G.add_edges_from([(1, 2), (2, 3), (3, 1), (1, 4)])

# 2. Compute the complement graph
G_complement = nx.complement(G)

# 3. Visualize both graphs
plt.figure(figsize=(12, 6))

# Plot original graph
plt.subplot(121)
pos = nx.spring_layout(G) # positions for all nodes
nx.draw_networkx_nodes(G, pos, node_color='lightblue', node_size=700)
nx.draw_networkx_edges(G, pos, width=2, edge_color='gray')
nx.draw_networkx_labels(G, pos, font_size=10, font_weight='bold')
plt.title('Original Graph (G)')
plt.axis('off')

# Plot complement graph
plt.subplot(122)
# Use the same positions for consistency
nx.draw_networkx_nodes(G_complement, pos, node_color='lightcoral', node_size=700)
nx.draw_networkx_edges(G_complement, pos, width=2, edge_color='darkred')
nx.draw_networkx_labels(G_complement, pos, font_size=10, font_weight='bold', font_color='black')
plt.title('Complement Graph (Ḡ)') # Unicode for G-bar
plt.axis('off')

plt.tight_layout()
plt.show()

Python code to create a graph, compute its complement, and visualize both using NetworkX and Matplotlib.

Handling Directed Graphs

The concept of a complement also applies to directed graphs (digraphs). For a directed graph G, its complement G' will have a directed edge (u, v) if and only if there is no directed edge (u, v) in G. NetworkX handles this seamlessly. The nx.complement() function works for both Graph (undirected) and DiGraph (directed) objects.

import networkx as nx
import matplotlib.pyplot as plt

# Create a directed graph
DG = nx.DiGraph()
DG.add_edges_from([('A', 'B'), ('B', 'C'), ('C', 'A')])

# Compute the complement of the directed graph
DG_complement = nx.complement(DG)

# Visualize both directed graphs
plt.figure(figsize=(12, 6))

# Plot original directed graph
plt.subplot(121)
pos_dg = nx.circular_layout(DG) # Use a different layout for variety
nx.draw_networkx_nodes(DG, pos_dg, node_color='lightgreen', node_size=700)
nx.draw_networkx_edges(DG, pos_dg, width=2, edge_color='darkgreen', arrowsize=20)
nx.draw_networkx_labels(DG, pos_dg, font_size=10, font_weight='bold')
plt.title('Original Directed Graph (DG)')
plt.axis('off')

# Plot complement directed graph
plt.subplot(122)
nx.draw_networkx_nodes(DG_complement, pos_dg, node_color='orange', node_size=700)
nx.draw_networkx_edges(DG_complement, pos_dg, width=2, edge_color='darkorange', arrowsize=20)
nx.draw_networkx_labels(DG_complement, pos_dg, font_size=10, font_weight='bold', font_color='black')
plt.title('Complement Directed Graph (DḠ)')
plt.axis('off')

plt.tight_layout()
plt.show()

Python code to compute and visualize the complement of a directed graph.