Inserting elements into Binary Min Heaps

Efficiently Inserting Elements into a Binary Min Heap

Learn the fundamental algorithm and implementation details for adding new elements to a binary min heap while maintaining its heap properties.

Binary heaps are a crucial data structure in computer science, widely used for priority queues, heap sort, and graph algorithms like Dijkstra's. A binary min heap is a complete binary tree where the value of each node is less than or equal to the values of its children. This property, known as the 'min-heap property', must be maintained after every operation, including insertion. This article will guide you through the process of inserting a new element into a binary min heap, ensuring the heap property is preserved.

Understanding the Min Heap Property

Before diving into insertion, it's vital to grasp the min-heap property. For any node N in the heap, if C is a child of N, then value(N) <= value(C). This means the smallest element is always at the root of the heap. Additionally, a binary heap is a 'complete' binary tree, meaning all levels are fully filled except possibly the last level, which is filled from left to right. This completeness allows for an efficient array-based representation where the children of a node at index i are at 2i + 1 (left child) and 2i + 2 (right child), and the parent of a node at index i is at (i - 1) / 2 (integer division).

graph TD
    A[Root: Smallest Element]
    B[Left Child]
    C[Right Child]
    A -- "value(A) <= value(B)" --> B
    A -- "value(A) <= value(C)" --> C
    B -- "value(B) <= value(D)" --> D[Left Grandchild]
    B -- "value(B) <= value(E)" --> E[Right Grandchild]
    style A fill:#f9f,stroke:#333,stroke-width:2px
    style B fill:#ccf,stroke:#333,stroke-width:2px
    style C fill:#ccf,stroke:#333,stroke-width:2px

Illustration of the Min Heap Property

The Insertion Algorithm: Add and Bubble Up

Inserting a new element into a binary min heap involves two main steps:

1. Add the new element to the end: To maintain the complete binary tree property, the new element is always added to the next available position in the heap, which is typically the last position in the underlying array representation.
2. "Bubble Up" (or "Heapify Up") the element: After adding the element, it might violate the min-heap property if its value is smaller than its parent's. To restore the property, the new element is repeatedly swapped with its parent until it reaches a position where it is greater than or equal to its parent, or it becomes the root of the heap. This process is also known as 'percolate up' or 'sift up'.

sequenceDiagram
    participant Heap
    participant NewElement

    Heap->>NewElement: Add new element to end of array/tree
    loop While NewElement < Parent
        NewElement->>Heap: Compare NewElement with Parent
        alt NewElement < Parent
            Heap->>NewElement: Swap NewElement with Parent
            NewElement->>Heap: Update current position to Parent's old position
        else NewElement >= Parent
            break
        end
    end
    Heap->>NewElement: Min-heap property restored

Sequence Diagram for Heap Insertion (Bubble Up)

Implementation Example (Python)

Let's look at a Python implementation of a min-heap with an insertion method. We'll use a list to represent the heap, where the root is at index 0.

class MinHeap:
    def __init__(self):
        self.heap = []

    def _parent(self, i):
        return (i - 1) // 2

    def _left_child(self, i):
        return 2 * i + 1

    def _right_child(self, i):
        return 2 * i + 2

    def insert(self, item):
        self.heap.append(item)
        self._heapify_up(len(self.heap) - 1)

    def _heapify_up(self, index):
        while index > 0 and self.heap[self._parent(index)] > self.heap[index]:
            parent_idx = self._parent(index)
            self.heap[parent_idx], self.heap[index] = self.heap[index], self.heap[parent_idx]
            index = parent_idx

    def peek(self):
        if not self.heap:
            return None
        return self.heap[0]

    def size(self):
        return len(self.heap)

# Example Usage:
min_heap = MinHeap()
min_heap.insert(10)
min_heap.insert(5)
min_heap.insert(15)
min_heap.insert(3)
min_heap.insert(8)

print(f"Heap after insertions: {min_heap.heap}") # Expected: [3, 5, 15, 10, 8]
print(f"Min element: {min_heap.peek()}") # Expected: 3

Python implementation of a MinHeap with an insert method.

Visualizing the Bubble Up Process

Let's trace an insertion. Suppose we have a min-heap [3, 5, 15, 10, 8] and we want to insert 2. The steps would be:

1. Add 2 to the end: The heap becomes [3, 5, 15, 10, 8, 2].
2. Bubble Up 2:
   • 2 (at index 5) is compared with its parent 15 (at index 2). 2 < 15, so they swap. Heap: [3, 5, 2, 10, 8, 15]. 2 is now at index 2.
   • 2 (at index 2) is compared with its parent 5 (at index 0). 2 < 5, so they swap. Heap: [2, 5, 3, 10, 8, 15]. 2 is now at index 0.
   • 2 is at the root (index 0), so the process stops. The heap property is restored.

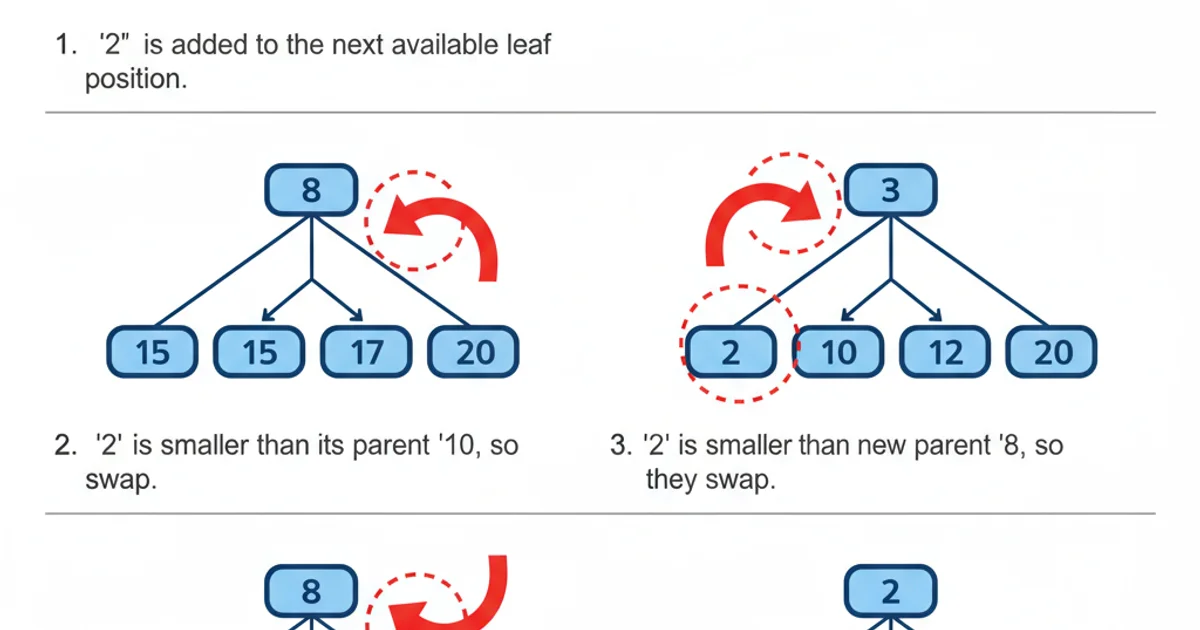
Step-by-step visualization of inserting '2' into a min-heap.