Complexity of Treemap insertion vs HashMap insertion

Treemap vs. HashMap: Understanding Insertion Complexity

Explore the fundamental differences in insertion complexity between Java's TreeMap and HashMap, and learn when to choose each for optimal performance.

When working with collections in Java, TreeMap and HashMap are two of the most commonly used implementations of the Map interface. While both store key-value pairs, their underlying data structures and, consequently, their performance characteristics—especially concerning insertion—differ significantly. Understanding these differences is crucial for writing efficient and scalable applications. This article delves into the time complexity of inserting elements into TreeMap and HashMap, providing insights into their internal mechanisms and practical implications.

HashMap Insertion: Average O(1)

A HashMap in Java is based on the principle of hashing. It stores key-value pairs in an array of linked lists (or balanced trees in Java 8+ for large buckets) called 'buckets'. When you insert an element, the hashCode() method of the key is used to determine the bucket index where the entry should be stored. Ideally, this process involves a constant number of operations: calculating the hash, finding the bucket, and adding the entry. This leads to an average time complexity of O(1) for insertion.

flowchart TD
    A["Start Insertion (HashMap)"] --> B{"Calculate Key's hashCode()"}
    B --> C["Determine Bucket Index"]
    C --> D{"Is Bucket Empty?"}
    D -- Yes --> E["Place Entry Directly"]
    D -- No --> F{"Handle Collision (Linked List/Tree)"}
    F --> G["Add Entry to Bucket"]
    G --> H["Check Load Factor & Resize (if needed)"]
    H --> I["End Insertion"]
    style A fill:#f9f,stroke:#333,stroke-width:2px
    style I fill:#f9f,stroke:#333,stroke-width:2px

HashMap Insertion Process Flow

However, the O(1) average case relies heavily on a good hash function and proper distribution of keys across buckets. If many keys hash to the same bucket (a 'collision'), the performance degrades. In the worst-case scenario, all keys might hash to the same bucket, turning the bucket into a long linked list or a tree. For a linked list, insertion becomes O(n), where 'n' is the number of elements in that bucket. For balanced trees (Java 8+), it becomes O(log n). The HashMap also needs to resize its internal array when the number of elements exceeds a certain 'load factor', which involves rehashing all existing elements and can be an O(n) operation.

import java.util.HashMap;

public class HashMapInsertion {
    public static void main(String[] args) {
        HashMap<Integer, String> hashMap = new HashMap<>();

        long startTime = System.nanoTime();
        for (int i = 0; i < 100000; i++) {
            hashMap.put(i, "Value" + i);
        }
        long endTime = System.nanoTime();
        long duration = (endTime - startTime) / 1_000_000;
        System.out.println("HashMap insertion for 100,000 elements: " + duration + " ms");

        // Example of poor hash function leading to collisions (conceptual)
        // For demonstration, imagine a custom class where all objects have same hashcode
        // MyKey key1 = new MyKey(1); // MyKey always returns 1 for hashCode()
        // MyKey key2 = new MyKey(2);
        // hashMap.put(key1, "Value1");
        // hashMap.put(key2, "Value2"); // This would cause collision and degrade performance
    }
}

TreeMap Insertion: O(log n)

A TreeMap in Java is implemented using a Red-Black Tree, which is a self-balancing binary search tree. This structure ensures that the tree remains balanced, preventing worst-case scenarios where it degenerates into a linked list. When you insert an element into a TreeMap, the key is compared with existing keys to find its correct position in the tree. This comparison process involves traversing the tree from the root to a leaf. Since the tree is balanced, the height of the tree is logarithmic with respect to the number of elements (log n). Therefore, inserting an element into a TreeMap always has a time complexity of O(log n).

flowchart TD
    A["Start Insertion (TreeMap)"] --> B{"Compare New Key with Root"}
    B -- New Key < Current --> C["Move Left"]
    B -- New Key > Current --> D["Move Right"]
    C --> B
    D --> B
    B -- Found Insertion Point --> E["Insert New Node"]
    E --> F["Perform Red-Black Tree Balancing Operations"]
    F --> G["End Insertion"]
    style A fill:#f9f,stroke:#333,stroke-width:2px
    style G fill:#f9f,stroke:#333,stroke-width:2px

TreeMap Insertion Process Flow

The O(log n) complexity for TreeMap insertion is consistent, regardless of the key distribution, because the tree structure is always maintained in a balanced state. This makes TreeMap a predictable choice for performance. However, it's generally slower than HashMap's average O(1) because each insertion involves multiple comparisons and potentially tree rotations to maintain balance, which are more computationally intensive than simple hash calculations and array access.

import java.util.TreeMap;

public class TreeMapInsertion {
    public static void main(String[] args) {
        TreeMap<Integer, String> treeMap = new TreeMap<>();

        long startTime = System.nanoTime();
        for (int i = 0; i < 100000; i++) {
            treeMap.put(i, "Value" + i);
        }
        long endTime = System.nanoTime();
        long duration = (endTime - startTime) / 1_000_000;
        System.out.println("TreeMap insertion for 100,000 elements: " + duration + " ms");
    }
}

Choosing Between TreeMap and HashMap

The choice between TreeMap and HashMap for insertion depends on your specific requirements:

• HashMap is generally faster for insertion when you don't need sorted keys and have a good hash function. Its average O(1) complexity makes it ideal for high-throughput scenarios where the order of elements is not important.
• TreeMap is preferred when you need keys to be stored in a sorted order. While its insertion complexity is O(log n), it provides ordered iteration over keys, which HashMap does not. This is useful for tasks like range queries or displaying data in a sorted manner.

Consider the trade-offs: HashMap offers speed at the cost of predictable order and potential worst-case performance with poor hash functions. TreeMap offers guaranteed logarithmic performance and sorted keys at the cost of being generally slower than HashMap for basic operations.

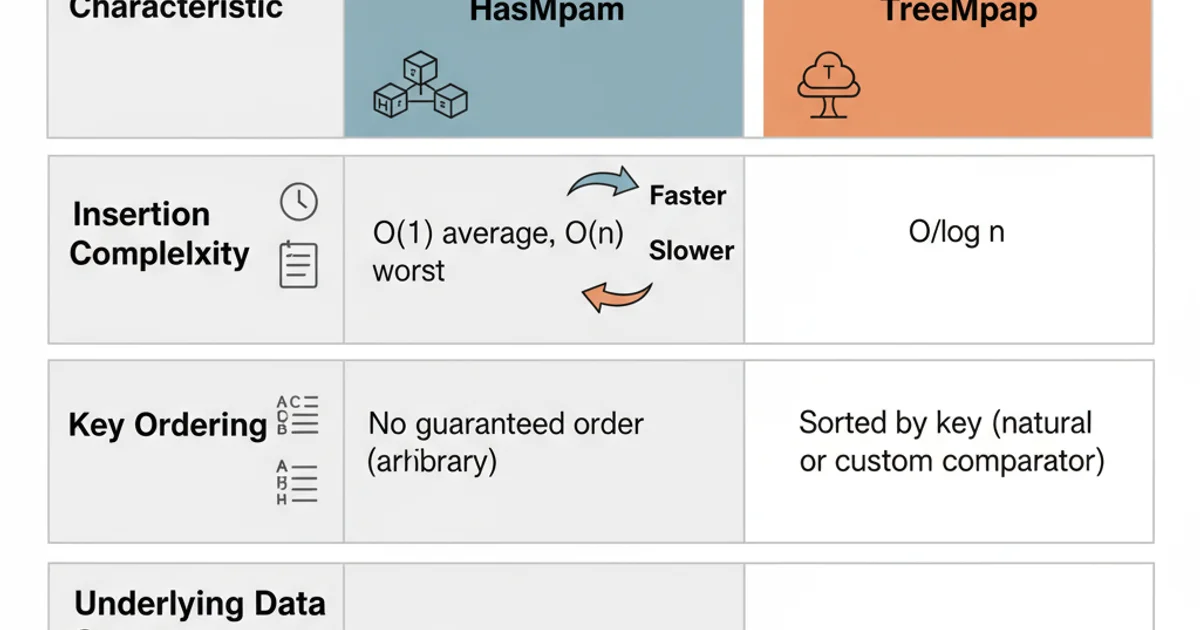
Key Differences: HashMap vs. TreeMap Insertion