Find words with most occurrence of each letter in the alphabet

Finding Words with the Most Occurrences of Each Letter in the Alphabet

Discover how to efficiently identify words that contain the highest count of each individual letter of the alphabet within a given text corpus using Java.

Analyzing text data often involves understanding the distribution and frequency of characters. A common challenge is to find, for each letter of the alphabet, the word that contains that letter the most times. This article provides a comprehensive guide to solving this problem using Java, focusing on clear logic, efficient data structures, and practical implementation.

Understanding the Problem and Data Structures

The core of this problem requires us to iterate through a collection of words and, for each word, count the occurrences of every letter from 'a' to 'z'. We then need to keep track of the word that holds the maximum count for each specific letter. This implies maintaining a mapping where each letter points to the word that currently has its highest count, along with that count itself.

flowchart TD
    A[Start with a list of words] --> B{Initialize Map: letter -> {word, count}}
    B --> C{For each word in list}
    C --> D{Count letter frequencies in current word}
    D --> E{For each letter 'a' through 'z'}
    E --> F{Compare current word's letter count with stored max}
    F -- If current > stored --> G[Update Map: letter -> {current word, current count}]
    F -- If current <= stored --> E
    G --> E
    E -- All letters processed --> C
    C -- All words processed --> H[Output Map contents]
    H --> I[End]

Flowchart illustrating the process of finding words with the most occurrences of each letter.

To achieve this, we can use a HashMap in Java. The keys of this map will be characters (representing the letters 'a' through 'z'), and the values will be custom objects or Map.Entry instances storing both the word and its highest count for that specific letter. This structure allows for efficient lookups and updates as we process each word.

Implementing the Solution in Java

Let's break down the implementation into key components: a helper method to count letter frequencies within a single word, and the main logic to iterate through all words and update our maximums. We'll use a simple LetterStats class to hold the word and its count for a given letter.

import java.util.HashMap;
import java.util.Map;

public class LetterOccurrenceFinder {

    // Helper class to store the word and its max count for a specific letter
    static class LetterStats {
        String word;
        int count;

        public LetterStats(String word, int count) {
            this.word = word;
            this.count = count;
        }

        @Override
        public String toString() {
            return "'" + word + "' (count: " + count + ")";
        }
    }

    /**
     * Counts the occurrences of each character in a given word.
     * @param word The input word.
     * @return A map where keys are characters and values are their counts.
     */
    private static Map<Character, Integer> countLettersInWord(String word) {
        Map<Character, Integer> charCounts = new HashMap<>();
        for (char c : word.toLowerCase().toCharArray()) {
            if (Character.isLetter(c)) {
                charCounts.put(c, charCounts.getOrDefault(c, 0) + 1);
            }
        }
        return charCounts;
    }

    /**
     * Finds the word with the most occurrences of each letter in a list of words.
     * @param words An array of words to analyze.
     * @return A map where keys are letters ('a' through 'z') and values are LetterStats objects
     *         containing the word with the highest count for that letter and the count itself.
     */
    public static Map<Character, LetterStats> findWordsWithMostLetterOccurrences(String[] words) {
        Map<Character, LetterStats> maxLetterOccurrences = new HashMap<>();

        // Initialize map with all letters and default stats
        for (char c = 'a'; c <= 'z'; c++) {
            maxLetterOccurrences.put(c, new LetterStats("", 0));
        }

        for (String word : words) {
            Map<Character, Integer> currentWordLetterCounts = countLettersInWord(word);

            for (Map.Entry<Character, Integer> entry : currentWordLetterCounts.entrySet()) {
                char letter = entry.getKey();
                int currentCount = entry.getValue();

                LetterStats storedStats = maxLetterOccurrences.get(letter);

                if (currentCount > storedStats.count) {
                    maxLetterOccurrences.put(letter, new LetterStats(word, currentCount));
                }
            }
        }
        return maxLetterOccurrences;
    }

    public static void main(String[] args) {
        String[] sampleWords = {
            "apple", "banana", "aardvark", "Mississippi", "programming",
            "jazz", "xylophone", "quizzical", "bookkeeper", "excellent"
        };

        Map<Character, LetterStats> results = findWordsWithMostLetterOccurrences(sampleWords);

        System.out.println("Words with most occurrences of each letter:");
        for (char c = 'a'; c <= 'z'; c++) {
            LetterStats stats = results.get(c);
            if (stats.count > 0) {
                System.out.println(c + ": " + stats);
            } else {
                System.out.println(c + ": No occurrence found");
            }
        }
    }
}

Java code for finding words with the most occurrences of each letter.

Analyzing Time and Space Complexity

Understanding the performance characteristics of our solution is crucial. Let's analyze the time and space complexity:

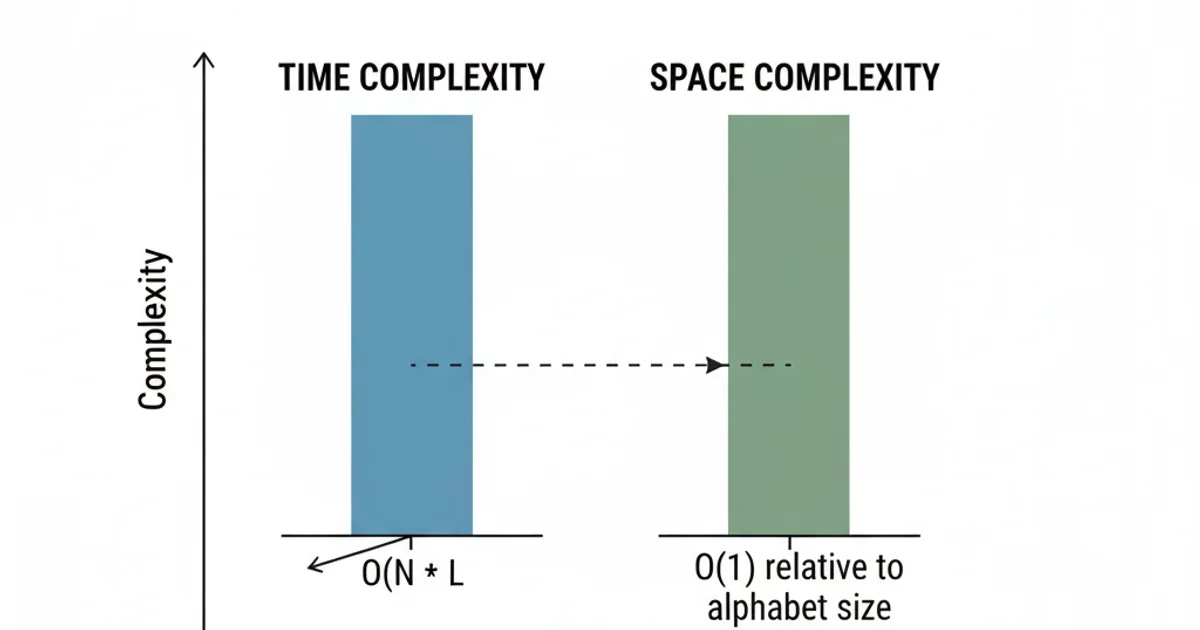
Visual representation of the algorithm's complexity.

Time Complexity:

1. Initialization: Initializing the maxLetterOccurrences map takes O(26) or O(1) time (constant, as the alphabet size is fixed).
2. countLettersInWord method: For each word, this method iterates through its characters. This takes O(L) time.
3. Main loop: We iterate N times (once for each word).
4. Inner loop: Inside the main loop, after counting letters for a word, we iterate through the entrySet() of currentWordLetterCounts. In the worst case, a word can contain all 26 unique letters, so this loop runs at most O(26) times, which is O(1).

Combining these, the total time complexity is approximately N * (L + 26), which simplifies to O(N * L). This is efficient as it processes each character of each word once.

Space Complexity:

1. maxLetterOccurrences map: This map stores 26 entries (one for each letter of the alphabet). Each entry stores a char, a String (the word), and an int (the count). The size of the word string can vary, but the number of entries is constant. So, O(26 * (size_of_word_string)) which is effectively O(1) relative to the input size, as the alphabet size is fixed.
2. currentWordLetterCounts map: This temporary map is created for each word and stores at most 26 entries. Its space is also O(1) relative to the alphabet size.

Therefore, the overall space complexity is O(1) (constant space) because the storage required does not grow with the number of words or their lengths, beyond the fixed size of the alphabet.